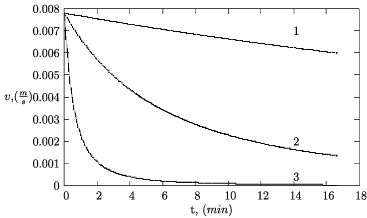
Curve 1 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^{ - 5}}$$
curve 2 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^6}$$
and curve 3 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^7}$$


Hai-Chao Wang1 Xiao-Ling Lei1* Vladimir Olennikov2
1Chongqing Academy of Science & Technology, China*Corresponding author: Xiao-ling Lei, Professor, Chongqing Academy of Science and Technology (CAST); No. 2, Yangliu Road, Huangshan Avenue, New North Zone, Chongqing, China 401123, E-mail: ellenlei2008@126.com
The simplest model of adsorbing of fouling for ultrafiltration is considered the simplest model of solutes adsorption and fouling for ultrafiltration was considered. Within framework of hydro dynamical approach the membrane resistance was obtained. The membrane resistance was obtained within a framework of hydrodynamics. It was found that membrane resistance is non-exponential function on membrane operation time. The membrane resistance was found to be a non-exponential function on operation time. We found that for a shot time of membrane operation the flux drops as a linear function. We found the flux drops as a linear function during a short time of membrane operation. For a long time t of operation the flux decline is proportional to t2.
Ultrafiltration; Membrane resistance
Ultrafiltration (UF) is a variety of membrane filtration in which forces like pressure or concentration gradients lead to a separation through a semi permeable membrane. Ultrafiltration (UF) is a type of membrane filtration in which pressure or concentration gradients separate through a semi-permeable membrane. Suspended solids and solutes of high molecular weight are retained in the so-called retentate, while water and low molecular weight solutes pass through the membrane in the permeate. During the process suspended solids of heavy molecular weight are retained while water and lighter molecular weight solutes pass through the membrane. This separation process is used in industry and research for purifying and concentrating macromolecular 103 ÷ 106 Da (Dalton) (1Da=1.660538921(73) •1027 kg is the unified atomic mass unit) solutions, especially protein solutions. Ultrafiltration is not fundamentally different from microfiltration. Both of these separate based on size exclusion or particle capture. Both processes segregate based on molecular size of particles. It is fundamentally different from membrane gas separation, which separate based on different amounts of absorption and different rates of diffusion. The process is different from membrane gas separations which segregate based on levels of absorption and diffusion. Ultrafiltration membranes are defined by the molecular weight cut-off (MWCO) of the membrane used. Ultrafiltration is applied in cross-flow or dead-end mode. The size of membrane interstices lies within range from 5 nm to 100 nm. The interstices membrane is within 5 nm to 100 nm.
At present, Ultrafiltration begins to play a significant role for drinking water production. In spite of the ultrafiltration grew fast during few last years, the membrane fouling problem is critical issue. Not sure what this means? The basic operating principle of ultrafiltration uses a pressure induced separation of solutes from water through a semi permeable membrane. The relationship between the applied pressure on the solution of water to be separated and the flux through the membrane is most commonly described by the Darcy Equation 1:
$$J\, = \,{{\Delta P} \over {\mu {R_t}}}\,\,\,\,\,\,\,\,\,\,.........(1)$$
where J=v is the flux (flow rate per membrane area), ΔP is the transmembrane pressure (pressure difference between feed and permeate stream), µ is the water viscosity, R2 is the total resistance (sum of membrane and fouling resistance). During the operating time of the membrane specific interactions between the membrane and the components in the raw water arise and cause a rapid and often irreversible fouling of membrane pores. A rapid and often irreversible fouling of the membrane pore is caused during ultrafiltration. As a consequence, the fouling resistance R growths and a rapid decline of flux J through the membrane takes place.
At present the processes of ultrafiltration are given detailed investigations [1-5]. In papers of Ho C-C et al. [6] and Andrianov AP et al. [7] the empiric formulae, which describe evolution of water flux J passing through the membrane, were obtained by using experimental data.
In our paper we apply the theoretical approach and consider the simplest model of UF membrane in order to obtain evolution of flux J with operating time t.
We investigate the dynamics of water Ultrafiltration flux within framework of hydrodynamical approach. We assume that a membrane with thickness l and area S has the n pores. Each interstice is a straight channel of cylindrical form with the diameter d and the length l. The total cross section area of all pores is $${S_n}\, = \,{{n\pi {d^2}} \over 4}$$ The continuity equation gives Equation 2
$$u{S_{n\,}}\, = \,\upsilon {S_n}\,\,\,\,\,{\rm{or}}\,\,\,\,\,\,u\, = \,\xi {\left( {{{{d_0}} \over d}} \right)^z}\upsilon \,\,\,\,........(2)$$
Where u is an average bulk velocity of water in the channel (within membrane) and is a velocity of water outside the membrane. We introduce the ratio between the area of membrane S and total cross section area of all pores for a clean membrane: $$\xi \, = \,{S \over {{S_{n0}}}},$$ where $${S_{no}}\, = \,{{n\pi {d_0}^2} \over 4}$$ and d0 is an initial diameter of the channel of a clean membrane.
We will describe the percolation of water through the membrane by the Bernoulli equation:
$$\Delta P\, = \,{\alpha _1}\,{{\rho {\upsilon ^2}} \over 2}\, + \,\lambda {l \over d}{{\rho {u^2}} \over 2}\, + \,{\alpha _2}{{\rho {\upsilon ^2}} \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...............(3)$$
Here P is a mass density of water, ΔP is the transmembrane pressure (pressure difference between feed and permeate stream), α1 is the resistance coefficient at the entrance of the interstice and α2 is the resistance coefficient at the outlet of the interstice; λ describes the resistance along the whole length. The Reynolds number for water flow in channel is
$${\mathop{\rm Re}\nolimits} \, = \,{{ud} \over \upsilon }\, = \,{{v{d_0}^2} \over {\upsilon d}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.............(4)$$
where ν is kinetic viscosity of water. For laminar flow in a channel the Reynolds number is smaller than 2300 and the coefficient of resistance λ is described by the Poiseuille formula. In opposite case, when the flow in the channel is a vortex, the coefficient of the resistance λ is described by the Altshul formula. So we can write:
$$\lambda \, = \,{\left\{ {^{{{64} \over {{\mathop{\rm Re}\nolimits} '}}}} \right._{0.11{{\left( {{\Delta \over d}\, + \,{{68} \over {{\mathop{\rm Re}\nolimits} }}} \right)}^{0.2s}}\,.{\mathop{\rm Re}\nolimits} \, > 2300}}{\,^{{\mathop{\rm Re}\nolimits} \, < 2300,}}\,\,\,\,\,\,\,\,\,\,\,\,..........(5)$$
Here Δ is an apparent roughness of the internal surface of the pores.
The diameter of membrane pore changes during the filtration process as a result of solutes adsorption at the internal surface of the pores. If the k is a coefficient of filtration (the ratio of adsorbed matter to solvent matter), we can suggest, that the mass adsorbed absorbed, please use spell check within a pore is proportional to the amount of permeate volume of purified water, that is
$$\dot m\,k{c_f}Sv,\,\,\,\,......(6)$$where cf is a concentration of solutes, J=V= Sυ is flux through the membrane. The point over symbols denotes derivation over time t. Following the authors of the paper [8] again state what’s in Katsoufidou’s paper, e.g [8] found that, we assume that fouling mass adsorbs uniformly forming a cylinder:
$$m\, = \,{\pi \over 4}\,\left( {{d_0}^2\, - \,{d^2}} \right)l{\rho _f}n,\,\,\,\,\,.....(7)$$
where ρf is the average mass density of the fouling adsorbed. Using (7) we can rewrite the equation (6) for d as
$$\dot d\, = \,{2 \over \pi }\,{{k{c_f}Sv} \over {\pi l{\rho _f}dn}}\, = \, - k{{{c_f}} \over {{\rho _f}}}\,{{\xi {d_0}^2} \over {2l}}\,{v \over {d'}}\,\,\,\,\,\,.....(8)$$
This differential equation is added to the initial condition d(0)=d0 . The equations (2-5), (8) describe process of raw water percolation through the Ultrafiltration membrane.
We assume that in the pore the Reynolds number Re<1 and the water flow is laminar. The coefficient λ is determined by the Poiseuille formula and the resistance along the whole length l is larger than α1 + α2 . Neglecting the terms with α1 and α2 we find the velocity of the flow from the equation (3):
$$v\, = \,{{P{d^4}\pi } \over {32\mu \xi {d_0}^2l}}\,\,\,\,\,\,\,.....(9)$$
Here µ=ρν is a dynamic solvent viscosity. Substituting (9) in the equation (8) and then integrating it the evolution of the diameter d with time t is found:
$$d(t)\, = \,{{{d_0}} \over {\left){\vphantom{1{1 + \,k{{{c_f}} \over {{\rho _f}}}{{\Delta P{d_0}^2} \over {32\mu {l^2}}}}}}\right.
\!\!\!\!\overline{\,\,\,\vphantom 1{{1 + \,k{{{c_f}} \over {{\rho _f}}}{{\Delta P{d_0}^2} \over {32\mu {l^2}}}}}}t}}\,\,\,\,\,\,\,........(10)$$
Evolution of the flux per unit area of membrane is
$$v(t)\, = \,{{\Delta P{d_0}^2} \over {32\mu \xi l{{\left( {1 + k{{{c_f}} \over {{\rho _f}}}{{\Delta P{d_0}^2} \over {32\mu {l^2}}}t} \right)}^2}}}\,\,\,\,\,\,......(11)$$
Comparing the equation (1) with the equation (11) we find the total resistance of the membrane:
$${R_t}\, = \,{{32\xi l} \over {{d_0}^2}}{\left( {1 + k{{{c_f}} \over {{\rho _f}}}{{\Delta P{d_0}^2} \over {32\mu {l^2}}}t} \right)^2}\,\,\,\,\,.....(12)$$
In this case the Reynolds number is
$${\mathop{\rm Re}\nolimits} \, = \,{{\Delta P{d_0}^2} \over {32\mu \upsilon l{{\left( {1 + k{{{c_f}} \over {{\rho _f}}}{{\Delta P{d_0}^2} \over {32\mu {l^2}}}t} \right)}^{{3 \over 2}}}}}\, \le \,{{\Delta P{d_0}^3} \over {32\mu \upsilon l}}\,\,\,\,\,......(13)$$
For real conditions, when a filtration pressure is 5•105 Pa, thickness of membrane is l=0.01 mm and the diameter of pores is d0 =100 nm, the dimensionless parameter is equal to
$${{\Delta P{d_0}^2} \over {32\mu \upsilon l}}\, = \,0.0015\,\,\,\,\,\,.....(14)$$
So, the Reynolds number Re<<1 in the pore and the parameter λl/d>>1. This means that our original suggestion that water flow is a laminar is realized.
We found that the resistance Rf (t) and the flux v(t) have non-exponential low. For a small time of operation, when inequality
$$t\, \ll \,{{{\rho _f}} \over {{c_f}}}\,{{32\mu {l^2}} \over {k\Delta P{d_0}^{2'}}}\,\,\,\,\,.....(15)$$
Holds, evolution of the total membrane resistance has linear law
$${R_t} = {{32\xi l} \over {d_0^2}}\left( {1 + 2k{{{c_f}} \over {{p_f}}}{{\Delta pd_0^2} \over {32\mu {l^2}}}t} \right)\,\,\,\,\,.........(16)$$
$${R_f}\, = \,{{32\xi } \over {{d_0}^2}}\,\,\,{\rm{is }}\,\,{\rm{the }}\,\,{\rm{resistance }}\,{\rm{of }}\,{\rm{a}}\,{\rm{ clean }}\,{\rm{membrane}}{\rm{.}}\,{\rm{ The}}\,{\rm{ flux }}\,{\rm{per }}\,{\rm{unit }}\,{\rm{area}}\,{\rm{ of}}\,{\rm{ membrane}}\,{\rm{ drops }}\,{\rm{as }}\,{\rm{a }}\,{\rm{linear }}\,{\rm{function:}}$$
$$v(t)\, \approx \,{{\Delta P{d_0}^2} \over {32\mu \xi l}}\,\left( {1 - 2k{{\Delta P{d_0}^2} \over {32\mu {l^2}}}t} \right)\,\,\,\,\,\,.........(17)$$
$${\rm{Hear}}\,v\, = \,{{\Delta P{d_0}^2} \over {32\mu \xi l}}\,{\rm{is }}\,{\rm{an}}\,{\rm{ initial }}\,{\rm{flux}}{\rm{. }}\,{\rm{For}}\,{\rm{ a}}\,{\rm{ long}}\,{\rm{ time }}\,{\rm{of }}\,{\rm{operation, }}\,{\rm{when }}\,{\rm{ inequality}}$$
$$t\, \gg \,{{{\rho _f}} \over {{c_f}}}{{32\mu {l^2}} \over {k\Delta P{d_0}^{2'}}}\,\,\,\,\,.......(18)$$
Holds, the total resistance of the membrane increases as t2 and equals
$${R_f}\, = \,{\xi \over {32{l^2}}}{\left( {k{{{\rho _f}} \over {{c_f}}}{{\Delta P{d_0}} \over \mu }} \right)^2}{t^2}\,\,\,\,\,......(19)$$
Water flux per through the membrane per unit area of membrane is
$$v(t)\, = \,{{32\mu {l^2}} \over {\xi \left( {k{{{c_f}} \over {{\rho _f}}}} \right)\Delta P{d_0}^2}}\,\,\,\,\,\,.......(20)$$
We can see that evolution of water flux is proportional to t-2. In figure 1 the results of calculations are presented for following parameters: $${d_0}\, = \,100\,nm,\,\,\Delta P\, = \,{10^5}\,Pa,\,\,k = 0.9,\,\,l = 0.01\,mm.$$
Curve 1 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^{ - 5}}$$
curve 2 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^6}$$
and curve 3 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^7}$$

Curve 1 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^{ - 5}}$$
curve 2 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^6}$$
and curve 3 shows flux evolution for $${{{c_f}} \over {{\rho _f}}}\, = \,{10^7}$$
One can see that for the curve 1 the inequality (15) holds, and flux drops as a linear function (17), while for the curve 3 the inequality (18) takes place, and flux drops as t-2 according to formula (20).
We considered evolution of water flux passing through the Ultrafiltration membrane. We applied the hydrodynamical approach and found that membrane resistance is a non-exponential function on membrane operation time. We found that for a short time of membrane operation the flux drops as a linear function. For a long time t of operation the flux decline is proportional to t-2.
Postdoctoral funding program of Chongqing (Rc201506); Technology Innovation Program of Chongqing Social Livelihood (cstc2015shmszx20015).
Download Provisional PDF Here
Article Type: Mini Review
Citation: Wang H-C, Lei X-L, Olennikov V (2016) The Dynamics of Water Ultrafiltration Flow within Framework of Hydrodynamical Approach. Int J Water Wastewater Treat 2(4): doi http://dx.doi.org/10.16966/2381-5299.125
Copyright: © 2016 Wang H-C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
All Sci Forschen Journals are Open Access