Abstract

Calcium phosphate bone cements have gained significant scientific and commercial attention due to their outstanding biological properties. In this work the cement's paste prepared by mixing a-TCP with sodium phosphate solution and the final hardening occurred after immersion in Ringer's solution. Their internal structure evolution from the hydrolysis of a-TCP to the formation of calcium deficient hydroxyapatite was observed my scanning electron microscopy. Time temperature superposition principle was applied in order to investigate their time- and temperature dependent dynamic response. It was found that time temperature superposition can be applied with success and that the material dynamic stiffness is time-and temperature dependent. Also, a nanostructure of hydroxyapatitic platelets and needles evolves within ten days, after specimen immersion for maturing in a Ringer’s solution. The resulting nanostructure was verified by means of scanning electron microscopy and x-ray diffraction techniques.

Keywords

Calcium phosphate; Bone cements; Hydroxyapatite; Time temperature superposition

Introduction

The process of bone fracture healing, is one of the most successful reconstructive process in the human body provided that the bone does not suffer multiple fragmentation. Substitution or reconstruction of massive bone deficiencies due to injuries, tumor removal or genetic disorders is a major clinical issue. As an alternative, a technique known as bone grafting is the procedure to fill bone defects with osteogenic or osteocοnductive materials with the objective of osseous regeneration. Ideal bone graft materials should exhibit properties such as: osteointegration, osteoconduction, osteoinduction and osteogenesis. Autografts or autogenous bone grafts taken from the patient’s body, usually satisfy all the above prerequisites. Autografts however, are supplied in limited quantities, let alone, they are also difficult to exctract from the patient since they demand surgical intervention. As a consequence, demand for different types of synthetic materials which exhibit osteointegrative and osteoconductive properties has led to many types of new biomaterials [1]. Several types of polymers, ceramics and bio-glasses are being used in osseous defects as bone substitutes. Calcium phosphate ceramics such as hydroxyapatite (HAP, Ca₁₀(PO₄ )₆ (OH)₂ ) or tricalcium phosphate (β-and α-TCP, Ca₃ (PO₄ )₂ ) are among the materials that gained attention and trust of the medical community in the last 10 years, are now widely applied in clinical practice, as bone fillers due to their excellent biocompatibility and osteoconductivity. Calcium phosphate bone cements (CPBCs) are also alloplastic materials which are used as bone substitutes [2]. An inherent problem of most of these materials are their relatively low mechanical properties especially in the case of bio-cements, glasses and polymers and adversely, the extremely higher sitffness of metals and ceramics with respect to bone tissue [3]. As far as the calcium phosphate cements are concerned, despite their excellent surgical and biological properties, they exhibit slow resorption rates of the apatite, which is usually the main product of the hardened cement [4]. One should add the processes of cement maturing and resorption by the organism, in order to fully understand the complex physico-chemical behavior of calcium phosphate cements in the presence of biological fluids.

In this work we employed a theoretical tool developed for polymeric materials, which are notorious of their time-relevant viscoelastic response. The aim of our work was to demonstrate by using the time temperature superposition principle (TTSP) that the character of calcium phosphate based biocements can be also described by such a model. Also, scanning electron microscopy was used to prove the evolution of nanostructure with time, in these materials.

Experimental Procedures

Calcium phosphate cements preparation

For the preparation of α-TCP powder, equimolar quantities of calcium carbonate and calcium pyrophosphate ball milled and next the mixture was placed in alumina crucible, dried at 80°C, placed in a furnace at 1300°C for 12 hours and rapidly quenched in air on a metallic surface. The resulted material was crushed in the ball mill. The cement powder was mixed with 4% w/v Na₂ HPO₄ solution in an agate mortar at a powder/ liquid ratio of 0.32 ml/gr.

Cement paste was casted into prismatic moulds, made from acrylic plastic, that had dimensions of 60 × 13 × 3.5 mm³ (width × height × length). The specimens remained in 100% humidity for 12 hours and were then removed from the mould and placed at 37°C in a polyethylene vial containing 60 ml of Ringer solution for 14 days for hardening. However, during hardening stage and at different time periods, prismatic specimens were recovered in couples, each time, from the isotonic solution and dried in an oven at 100°C for two hours in order to stop any reaction in progress. These time periods concerned the first hours of immersion and specifically 48,72,96,144,192 and 240 hours (2-10 days) respectively. It has been demonstrated that the micro structural changes take place and evolve within 12-15 days of immersion in aqueous media.

Dynamic mechanical analysis

In order to perform the TTSP analysis a Dynamic Mechanical Analyzer (DMA) Q800 of TA Instruments was employed. Specimens in the form of slabs with nominal dimensions of 60 ×13 × 3.2 mm³ were loaded under creep in three point bending mode to obtain TTSP data. Frequency was ranged from 1E-3 to 200 Hz at 10 points per decade temperature resolution, and Temperature was varied from 25-300°C at a heating rate of 3°C/min. Experimental DMA test set-up is shown in Figure 1.

Scanning Electron Microscopy (SEM)

Scanning Electron Microscopy pictures were taken from cryo-fractured specimens in order to study their internal nanostructure. Scans were obtain on carbon coated specimens in a JEOL 6510 Tungsten filament SEM.

Scanning Electron Microscopy pictures were taken from cryo-fractured specimens in order to study their internal nanostructure. Scans were obtain on carbon coated specimens in a JEOL 6510 Tungsten filament SEM.

All solids, including the reactants and the hardened cements were characterized by X-ray diffraction (XRD, Siemens/Bruker D5000) with CuKα radiation.

Theoretical Background of Time Temperature Superposition Principle (TTSP)

Time Temperature Superposition Principle (TTSP) [5] is reported, that it was presumably first observed by Leaderman [6] and theoretically summarised by Markovitz [7]. Based on his observations the creep compliance vs. log (time) curves for different temperatures for different materials retain the same shape. Also, increasing temperature has the effect of contracting the time scale and reducing temperature has the adverse effect. Tobolsky and Andrews [8] applied Leaderman's observations for the first time in order to superimpose the individual creep curves into a unique reference mother-curve.

Since then, TTSP has been used extensively as reported in the literature [5-21] for polymers and composite materials.

On the other hand, TTSP has been used to obtain the master curves for other viscoelasticmaterial properties such as creep, creep compliance and stress compliance against time (or log (time)) or dynamic modulus against frequency etc. [5].

As a rule of thumb when the TTSP is applied to the generation of a creep master curve the following methodology is followed.

• A material specimen is subjected to a constant load at a pre-set temperature level as in conventional creep testing, and the evolution of the creep strain of the specimen is recorded vs. the log (time), shown diagrammatically in Figure 1a.
• Parallel experiments are performed for different specimens or even the same specimen, in modern DMA equipment, at different temperature levels and the relevant creep curves are obtained.
• A desired reference temperature is selected (T_ref).
• All the individual creep curves corresponding to different temperature levels are shifted along the log (time) scale to be superimposed to a master or mother curve.

In some polymers, especially “simple” materials such as poly-isobutylene and other amorphous thermoplastics that have few complicating features in their microstructure, the relation between time and temperature can be described by correspondingly simple models. Such materials are termed “thermorheologically simple”, which is a prerequisite of the method.

A “time-temperature shift factor” α(T) can be defined as the horizontal shift that must be applied to a response curve Χ(Τ), measured at an arbitrary temperature T in order to move it to the curve measured at some reference temperature T_ref .

Figure 1: Top (a), side (b) and perspectice (c) view of the CaP specimen placed in the three point bending jigs of the DMA Q800 analyzer (d)

Then:

$$\log {a_T} = \log X\left( T \right) - \log X\left( {{T_{ref}}} \right)...........{\rm{Equation 1}}$$

To illustrate the shifting process more clearly two individual shear moduli curves are schematically shown in Figure 2. The same procedure is applicable to the other curves at different temperature levels. TTSP success depends on the smoothness at the overlap where two different individual curves meet. The great gain is that, if the TTSP method is valid, the master curve represents the true behaviour of a long-term test at the reference temperature.

Many researchers have investigated the temperature dependent behaviour of the horizontal shift factor and proposed various empirical formulas. Often, the WLF equation (Williams-Landel-Ferry) is used [4], but it is restricted to materials above the glass transition temperature (T_g ).

The WLF Equation 2 is:

$$\log {a_T} = - {{{C_1}\left( {T - {T_{ref}}} \right)} \over {{C_{2 + }}\left( {T - {T_{ref}}} \right)}}{\rm{......Equation 2}}$$

Where: C₁ and C₂ are arbitrary material constants whose values depend on the material and choice of reference temperature T_ref. It has been found that if T_ref is chosen to be T_g (polymer glass transition), then C₁ and C₂ often assume “universal” values applicable to a wide range of polymers.

Since calcium phosphate biocements do not display a glass transition, but remain crystalline at all temperatures, the relationship between the temperature and the horizontal shift factor, log (a_T), was calculated both based on the Arrhenius Equation 3 and the WLF models.

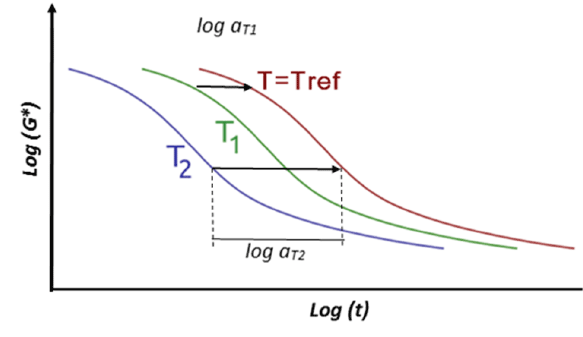
Figure 2: Applying of the Time Temperature Superposition Principle for a viscoelastic parameter (complex shear modulus) showing the shifting factors a_T

$$\log {a_T} = {E \over {2.303R}}\left( {{1 \over T} - {1 \over {{T_{ref}}}}} \right).........{\rm{Equation 3}}$$

Where: E: is the activation energy; R: is the universal gas constant; T: is the absolute temperature

An additional factor, which is not tested in this paper but could be tested by these methods, is that the master curve should be independent of the TTSP test regime adopted. The same curve should be produced from tests carried out for different durations or at different temperatures.

If it is possible to generate a smooth master curve by applying a horizontal shift along the log (time or temperature) axis, the material can be then characterized as a thermorheologically simple material (TSM). However, for some materials a vertical shift factor may be needed to obtain a smooth master curve; they are then classified as thermorheologically complex materials (TCM).

Although TTSP has been used for many decades for polymeric materials, no solid rules have been developed for obtaining the master curves. Usually, TTSP results exhibit the success of the method. Apart from polymer composites of various types [22], it has been successfully applied by quite a few researchers, to investigate a variety materials when time related or temperature activated procedures come into play. For example it has been successfully employed for the characterization of asphalt concrete [23], viscous metallic liquids [24], solid rocket propellants [25], wood [26], super cooled liquids [27], atomic force microscopy [28,29] and also to dielectric spectroscopy studies [30,31].

In our work, we apply this type of viscoelastic modeling to a material which is not a polymer but with a strong time-dependent character, due to its internal structure rearrangement i.e. crystalline phase transformation. For the first time it is applied to calcium phosphate bone cements to show their time-dependent behaviour. Our basic assumption is that these materials exhibit linear viscoelastic behavior. It has been already established that within 14 days these materials undergo significant structural changes [20,21], which can presumably alter their mechanical response with time.

Results and Discussion

Time temperature superposition analysis

Typical DMA spectra of Storage Moduli and tanδ parameters as a function of frequency are shown in Figure 3 for the CaP specimens. As it can be easily observed, there exists both effects of time (frequency) as well as temperature in these materials. Storage moduli tend to rise with rising testing temperature (bottom to top lines) and are also their values are climbing by almost 500 MPa within the range of chosen frequencies. The typical, as known from polymer materials, sigmoidal curve is easy to observe. So, although our material is not of polymeric nature, it still exhibits, interestingly, a “viscoelastic” time-temperature dependent response. Damping constant, tanδ, is also appearing to be influenced by both the variation of frequency and temperature, though at a rather smaller scale. Afterall, these are materials of ceramic composition and damping constants remain at low levels. Some anti-resonance effects, for both parameters, can be seen around 75 Hz and 100 Hz, at some temperatures, owing to specimen geometry and relative high stiffness.

By plotting the same DMA-determined spectra as functions of temperature, as seen in Figure 4, more or less the same observations are valid. Storage moduli tend to rise with increasing frequency even at 37°C, while temperature shows a deteriorating effect, not very pronounced, on the dynamic stiffness. Tanδ appears now rather insensitive to temperature variations.

TTSP method was applied on the data determined by DMA as presented above in Figures 3 and 4. The TTSP results with respect to time shifting are shown in Figure 5 up to 1000 s and at T_ref = 75°C indicatively, although data can be projected to very extensive time points. However, it can be already easily observed, that the compliance vs time of the calcium phosphate tends to rise implying changes in their internal structure with time. This is a very strong indication of maturing for these cements. Loss compliance though the scatter shown does not reflect any significant changes whereas tanδ already at 1000 s starts to become lower. So, an internal relaxation mechanism is evident from these curves as determined by TTSP. Effects of increased temperature as produced by TTSP are presented in Figure 6. The most pronounced effect here is the increase of material compliance, in other words the material becomes less stiff with temperature. This could be attributed to the evaporation of chemically bound water in the crystalline apatitic structure of the CaP cement. The effect is not so pronounced in loss compliance and also for tanδ values a small reduction with increasing temperature can be observed.

The validity, as well as the quality of the TTSP application to CaP bone cements can be determined by plotting the shift factors with temperature as shown in Figure 7. All shift factors are then fitted with both the Arrhenius and William-Landel-Fery equations. As observed, both equations pass through the experimental data, with satisfying accuracy. So, both equations can be used to predict by TTSP the long term material response.

The validity, as well as the quality of the TTSP application to CaP bone cements can be determined by plotting the shift factors with temperature as shown in Figure 7. All shift factors are then fitted with both the Arrhenius and William-Landel-Fery equations. As observed, both equations pass through the experimental data, with satisfying accuracy. So, both equations can be used to predict by TTSP the long term material response.

SEM nanostructural observations

SEM observations revealed remarkable evidence on the evolution of the CaP bone cements micro and nanostructures. As seen from the microphotographs presented in Figure 8, the bone cements show spherical aggregates composed of nanoscale grains even 3 days after being immersed in Ringer’s solution. Between 3 and 6 days (72-144 hrs) maturing a pronounced microstructure evolves in the form of microplatelets of calcium deficient hydroxyapatite [32]. This microstructure continuous to evolve and within 6-8 days from immersion nanoplateletes and needles start to grow due to transformation reaction of a-TCP to calcium deficient apatite. After 14 days the whole internal structure has been transformed to nano-apatitic crystals as shown in Figure 9. These findings corroborate the conclusions from DMA testing and TTSP modeling that CaP bone cements present a time dependent dynamic mechanical response, obviously due to the continuous evolution of a micro to nanostructure.

Further, Figure 10 depicts the XRD patterns of hardened cement together with the JCPDS standard card of hydroxyapatite. The diffraction peaks of the cement are fitted to the standard hydroxyapatite card peaks. An interesting feature in Figure 10 is that that the peaks correspond to (211), (112) and (300) reflections are overlapped due to peak broadening. This suggests lower crystallinity which can be attributed with the presence of foreign ions in the structure like carbonate and also with the formation of calcium deficient (nonstochiometric) hydroxyapatite [3].

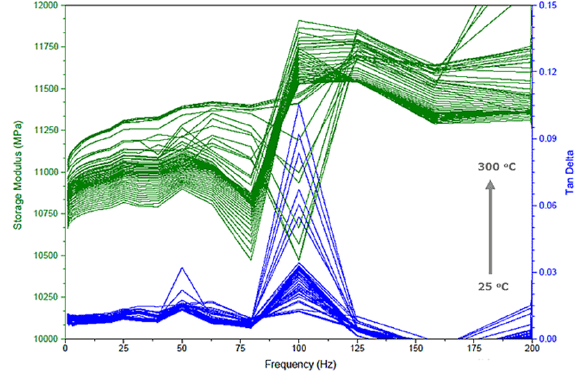
Figure 3: Storage (left y-axis), tanδ (right y-axis) as functions of frequency from the TTSP analysis-raw data

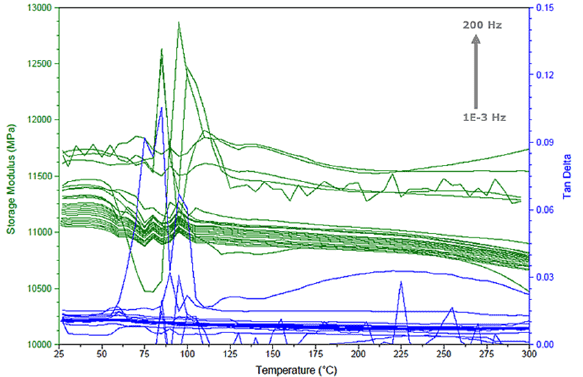
Figure 4: Storage (left y-axis), tanδ (right y-axis) as functions of temperature from the TTSP analysis-raw data

Conclusions

Dynamic Mechanical Analysis was performed in Calcium Phosphate bone cements. The results indicate an effect of storage moduli reduction at temperatures below 100°C owing probably to loss of chemically bound water in the cement mass.

No significant effect was observed in loss moduli of the tested material mainly due to the ceramic nature of the tested material. Material damping ratio showed limited sensitivity to time and temperature.

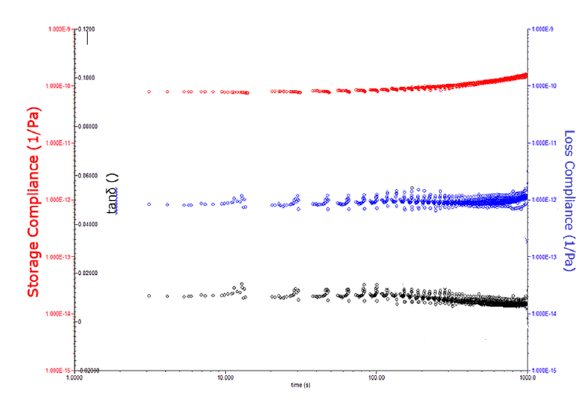
Figure 5: Storage compliances (left y-axis), tanδ (left inner y-axis) and Loss compliances as functions of time from the TTSP analysis, T_ref = 75°C

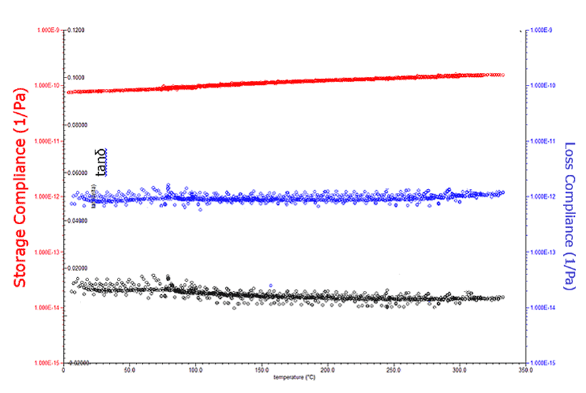
Figure 6: Storage compliances (left y-axis), tanδ (left inner y-axis) and Loss compliances as functions of temperature from the TTSP analysis

TTSP was also applied in the Calcium Phosphate bone cements. It was observed that within tight temperature margins, the TTS principle could be successfully applied giving long term predictions for the dynamic properties of such materials. Corroborated by SEM observations and verified by XRD spectra, it was shown that the evolution of an internal nanostructure produces a time-dependent dynamic mechanical material response with time.

Acknowledgements

This research has been co-financed by the European Union (European Social Fund-ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF)-Research Funding Program: THALES, and within the context of MIS 379380 research project.

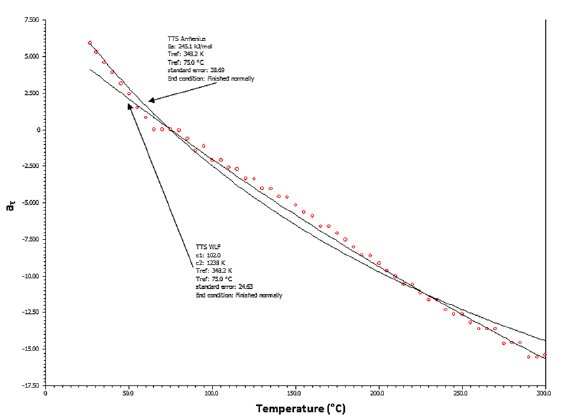
Figure 7: Variation of the temperature shift factor aτ as a function of temperature for Arrhenius and William-Landel-Ferry models respectively

Figure 8: SEM images showing the internal nano-structure evolution of the CaP bone cements

Figure 9: SEM image exhibiting the hydroxyapatite nanoplatelet and structure of the hardened bone cements

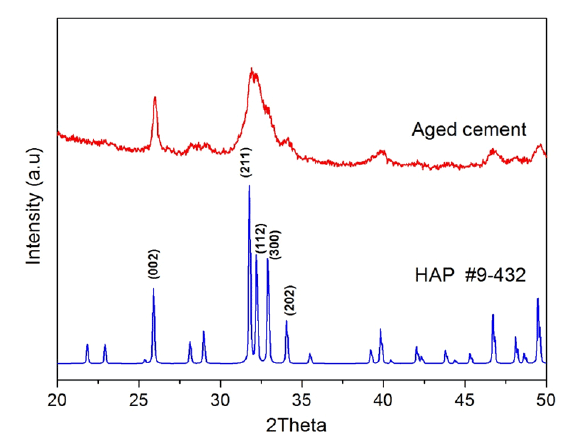
Figure 10: XRD patterns of hardened cement after immersion in Ringer’s solution for 14 days and JCPDS standard card of hydroxyapatite

References

1. Moore WR, Graves SE, Bain GI (2001) Synthetic bone graft substitutes. ANZ Journal of Surgery 71: 354-361. [Ref.]
2. Vallet-Regi M, González-Calbet JM (2004) Calcium phosphates as substitution of bone tissues. Progress in Solid State Chemistry 32: 1-31. [Ref.]
3. Alexopoulou Μ, Mystiridou Μ, Mouzakis D, Zaoutsos S, Fatouros DG, et al. (2015) Preparation, characterization and in vitro assessment of ibuprofen loaded calcium phosphate/gypsum bone cements. Cryst Res Tech. DOI: 10.1002/crat.201500143 [Ref.]
4. Roach P, Eglin D, Rohde K, Perry CC (2007) Modern biomaterials: a review-bulk properties and implications of surface modifications. J Mater Sci Mater Med 18: 1263-1277. [Ref.]
5. Ferry JD (1980) Viscoelastic properties of polymers. 3rd Edition John Willey and Sons, Inc ISBN: 978-0-471-04894-7. [Ref.]
6. Leaderman H (1943) Elastic and Creep Properties of Filamentous Materials. Textile Foundation, Washington DC, USA. [Ref.]
7. Markovitz H (1975) Superposition in rheology. J Polym Sci Symposium 50: 431–456. [Ref.]
8. Tobolsky AV, Andrews RD (1945) Systems manifesting superposed elastic and viscous behavior. J Chem Phys 13: 3-27. [Ref.]
9. Brinson HF, Morris DH, Yeow YT (1978) A new experimental method for the accelerated characterisation and prediction of the failure of polymer-based composites laminates. 6th International Conference for Experimental Stress Analysis, Munich, West Germany.
10. Griffith WI (1980) The accelerated characterization of viscoelastic composite materials. PhD Thesis submitted to the Virginia Polytechnic Institute and State University, USA. [Ref.]
11. Dutta PK, Hui D (2000) Creep rupture of a GFRP composite at elevated temperatures Composites and Structures. Computers and Structures 76: 153-161. [Ref.]
12. Marsimov RD, Plume E (1982) Predicting the creep of unidirectional reinforced plastics with thermorheologically simple structural components. Mech Comp Mater 18: 737-744. [Ref.]
13. Marsimov RD (1984) Prediction of the long-term resistance of polymer composites. Mech Comp Mater 20: 376-388. [Ref.]
14. Jeon HY, Kim SH, Yoo HK (2002) Assessment of long-term performances of polyester geogrids by accelerated creep test. Polym Test 21: 489-495. [Ref.]
15. Povolo F (1985) Scaling relationships in a constitutive equation with one structure variable. J Mater Sci Let 4: 619-623. [Ref.]
16. Povolo F, Fontelos M (1987) Time-temperature superposition principle and scaling behaviour. J Mater Sci 22: 1530-1534. [Ref.]
17. Povolo F, Hermida EB (1991) Analysis of the master curve for the viscoelastic behaviour of polymers. Mechanics of Materials 12: 35-46. [Ref.]
18. Hermida EB, Povolo F (1994) Analytical-numerical procedure to determine if a set of experimental curves can be superimposed to form a master curve. Polymer Journal 26: 981-992. [Ref.]
19. Brinson LC, Gates TS (1995) Effects of physical aging on long term creep of polymers and polymer matrix composites. Int J Solids and Struct, 32: 827-846. [Ref.]
20. Ginebra MP, Fernández E, De Maeyer EA, Verbeeck RM, Boltong MG, et al. (1997) Setting reaction and hardening of an apatitic calcium phosphate cement. J Dent Res 76: 905-912. [Ref.]
21. Komlev VS, Fadeeva IV, Barinov SM, Rau JV, Fosca M, et al. (2012) Phase development during setting and hardening of a bone cement based on α-tricalcium and octacalcium phosphates. J Biomater Appl 26: 1051-1068. [Ref.]
22. Georgiopoulos P, Kontou E (2015) Τhe effect of wood-fiber type on the thermomechanical performance of a biodegradable polymer matrix. J Appl Polym Sci 132: 42185. [Ref.]
23. Schwartz C, Gibson N, Schapery R (2002) Time-Temperature Superposition for Asphalt Concrete at Large Compressive Strains. Transportation Research Record: J Transportation Research Board 1789:101-112. [Ref.]
24. Meyer A, Busch R, Schober H (1999) Time-Temperature Superposition of Structural Relaxation in a Viscous Metallic Liquid. Phys Rev Lett 83: 5027-5029. [Ref.]
25. Jeremic R (1999) Some Aspects of Time-Temperature Superposition Principle Applied for Predicting Mechanical Properties of Solid Rocket Propellants. Propellants Explosives Pyrotechnics 24: 221–223. [Ref.]
26. Samarasinghe S, Loferski JR, Holzer SM (1994) Creep modeling of wood usingTime-temperature superposition. Wood and Fiber Science 26: 122-130. [Ref.]
27. Gleim T, Kob W, Binder K (1998) How Does the Relaxation of a Supercooled Liquid Depend on Its Microscopic Dynamics? Phys Rev Lett 81: 4404. [Ref.]
28. Zou S, Schönherr H, Vancso GJ (2005) Force Spectroscopy of Quadruple H-Bonded Dimers by AFM: Dynamic Bond Rupture and Molecular Time−Temperature Superposition. J Am Chem Soc 127: 11230–11231. [Ref.]
29. Bertrand-Lambottea P, Loubeta JL, Verpy C, Pavana S (2001) Nanoindentation, scratching and atomic force microscopy for evaluating the mar resistance of automotive clearcoats: study of the ductile scratches. Thin Solid Films398-399: 306–312. [Ref.]
30. Anantha PS, Hariharan K (2005) AC Conductivity analysis and dielectric relaxation behaviour of NaNO3 –Al2 O3 composites. Materials Science and Engineering: B 121:12-19. [Ref.]
31. Zhao J, McKenna GB (2012) Temperature divergence of the dynamics of a poly(vinyl acetate) glass: Dielectric vs. mechanical behaviors. J Chem Phys 136: 154901. [Ref.]
32. Andriotis O, Katsamenis OL, Mouzakis DE, Bouropoulos N (2010) Preparation and characterization of bioceramics produced from calcium phosphate cements. Cryst Res Tech 45: 239–243. [Ref.]

Download Provisional PDF Here

 

Article Information

Aritcle Type: Research Article

Citation: Mouzakis DE, Bouropoulos N, Rokidi S, Zaoutsos SP (2015) Time Dependent Properties of Nanocomposite Hydroxyapatite Based Bone Cements. Int J Nanomed Nanosurg 1(2): http:// dx.doi.org/10.16966/2470-3206.105

Copyright: © 2015 Mouzakis DE, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Publication history: 

Received date: 21 October 2015

Accepted date: 6 Nov 2015

Published date: 10 Nov 2015