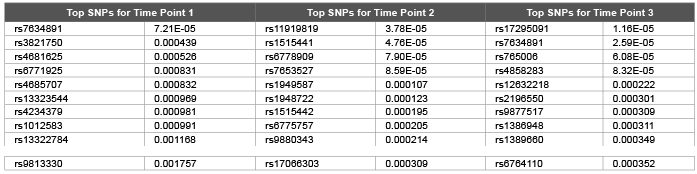
Table 1: Top 10 SNPs and correspondent raw p values obtained using random walk model from genomic relationship matrix for first replicate of DBP

Burak Karacaören*
Department of Animal Science, Faculty of Agriculture, Akdeniz University, Antalya, Turkey*Corresponding author: Burak Karacaören, Department of Animal Science, Faculty of Agriculture, Akdeniz University, Antalya, Turkey, E-mail: burakkaracaoren@akdeniz.edu.tr
Linear mixed model with pedigree information commonly employed to detect and correct for genetic relationship in cross sectional genomics research. Main aim of this study was to dynamic association mapping by using a random walk-Kalman filter approach for analyzing GAW18 dataset. We also extended the model to incorporate stationary process by auto regressive structure for dynamic gene and environmental effects.
We used random walk model and it is given below
$${y_t} = {a_t} + {\varepsilon _t},{\varepsilon _t} \propto N\left( {O,\sigma _e^2} \right);{a_{t + 1}} = {a_t} + {\eta _t},{\eta _t} \propto {\mkern 1mu} N\left( {O,A\sigma _n^2} \right)$$ In (1) the first equation is called the observation equation and the second equation is called the state equation. We assumed that observations, yt , depends on unobservable quantity, αt , and our aim was to do statistical inference on αt (states)
Error, genetic and permanent environmental variance components were predicted as 17.3 (0.0006), 10.9 (0.0007) and 8.2 (0.0006) using genomic relation matrix for and 18.0 (0.0007), 9.2 (0.0008) and 8.4(0.0006) using pedigree relation matrix for diastolic blood pressure. Rs 11711953 from time point 1, 2 and 3 is found to be associated with MAP4 gene.
Probably due to small number of time points the model did not detect all true genomic signals. Genomic relationship matrix gave better inflation factors. Random walk is a non stationary process and in this paper we extended the model for stationary case by tuning ∆ parameter. In genomic studies failing to taken into account of longitudinal gene and environmental effects over time may lead to either undetection of true signals and/ or may also lead to false positives due to stochastic errors.
Association mapping; Random walk; Kalman filter; Gibbs sampling
Mixed model approach with pedigree information commonly employed to detect and correct for genetic relationship in cross sectional genomics research [1]. Since gene expression may change over time repeated measures would be more useful for detecting associated genomic signals [2]. Dynamic association studies commonly use functional mapping approach. However interpreting results from regression coefficients of (non) parametric functions may be difficult biologically. Random regression coefficient model was suggested for dynamic association mapping [3]. However random regression models have limitations for obtaining accurate estimates at the beginning and end of the trajectories [4].
In addition both of the mentioned models (and those others in the literature of dynamic association mapping) needs whole set of observations in order to have predictions: this may also create problem as such to wait for months (if not years) to obtain predictions. In this study we assumed that genomic signal over time could be traced by a random walk- Kalman filter model in state space form to obtain longitudinal residuals. Because of the Kalman filter we do not have to wait for collecting the whole data set to do model evaluations hence estimates becomes available as soon as measurements are taken. And because of longitudinal residuals to employ in association mapping: biological reasoning could also be deduced easily given the signal is genuine.
Recently, we extended the GRAMMAR model of [1] in Bayesian context [5]. In this paper we used [6] model for dynamic association mapping by including dynamic components using random walk-Kalman filter approach to analyze GAW18 dataset. We also extended the model to incorporate stationary process by auto regressive structure for dynamic gene and environmental effects.
GAW 18 provided simulated phenotypes for 200 replicates from 849 individuals by 3 time points. We used Diastolic Blood Pressures (DBP) phenotype for association mapping. We analyzed 65519 SNPs from chromosome 3 using related 849 individuals for 3 time points of the first replicate.
We used 849 pedigreed individuals from chromosome 3 with 65519 SNPs for association mapping. We excluded 7229 SNPs due to minor allele frequency <1%, 208 SNPs due to Hardy Weinberg test (p<0.001), and 2 SNPs due to missingness test (p>0.1) leaving 58080 SNPs in the analyses [7]. We excluded 44 individuals with too low genotyping leaving 805 individuals in the dataset. Kolmogrow-Smirnow test used to assess normality of the response variables. Time, Sex, smoking status, age and pedigree number was included as a fixed effect in subsequent analyses based on preliminary analyses using correlations between predictions and observations.
We used random walk model and it is given below
$${y_t} = {\alpha _t} + {\varepsilon _t},{\varepsilon _t} \propto N(0,\sigma _e^2)$$
$${\alpha _{t + 1}} = {\alpha _t} + {\eta _t},{\eta _t} \propto N(0,\sigma _n^2)............(1)$$
In (1) the first equation is called the observation equation and the second equation is called the state equation. We $$\eqalign{ & assumed\,{\rm{ }}that\,{\rm{ }}observations\,{y_t},\,{\rm{ }}depends\,{\rm{ }}on\,{\rm{ }}unobservable\,{\rm{ }}quantity\,{\alpha _t},{\rm{ }}\,and\, \cr & {\rm{ }}our\,{\rm{ }}aim{\rm{ }}\,was\,{\rm{ }}to\,{\rm{ }}do\,{\rm{ }}statistical\,{\rm{ }}inference\,{\rm{ }}on\,\,{\alpha _t}\left( {states} \right).\,{\rm{ }}We\,{\rm{ }}assumed\,{\rm{ }}constant\, \cr & {\rm{ }}variances\,{\rm{ }}for\,{\varepsilon _t}and\,{\eta _t}\,as\,\,\sigma _e^2and\,\sigma _n^2\,respectively\,{\rm{ }}with\,{\rm{ }}independent, \cr} $$ identically and normally distributed random variables with zero means. We assumed that both gene effects and permanent environmental effects.
For genetic analyses of traits following mixed model is used;
$$y = X\beta + {Z_a}a + {Z_p}p + e................(2)$$
where y is the vector of observations, β is the vector of fixed effects, a is the vector of random effects, p is the vector of random permanent environmental effects, X, Za , Zp are design matrices and e is the vector of random $$\eqalign{ & residual\,{\rm{ }}effects.\,\sigma _a^2\,,\,\sigma _p^2\,{\rm{,}}\,{\rm{ }}and\,\sigma _e^2\,;\,{\rm{ }}are\,{\rm{ }}genetic,\,{\rm{ }}permanent\,{\rm{ }}environment\,{\rm{ }}and\,{\rm{ }}error\, \cr & {\rm{ }}variances.\,A\,is\,{\rm{ }}the\,{\rm{ }}additive \cr} $$ genetic relationship matrix for the individuals; is an identity matrix. A was obtained by the coefficient of coancestry matrix using both the genotype and pedigree of individuals.
In the following, we show general assumptions used in KF-RW method, based on Bayesian principles. Proportional joint posterior distribution without constant terms given in (3) using (2) based on following recursive relationship [8];
$$p\left( {{\theta _t}\left| {{\theta _{\left( { - t} \right)}},{Y_n}} \right.} \right) \propto p\left( {{\theta _t}\left| {{\theta _{\left( {t - 1} \right)}},{Y_{t - 1}}} \right.} \right)p\left( {{\theta _{t + 1}}\left| {{\theta _t},{Y_{t - 1}}} \right.} \right)p\left( {{{\rm{Y}}_t}\left| {{\theta _t},{Y_{t - 1}}} \right.} \right),$$
$$f\left( {y/b,a,p,\sigma _a^2,\sigma _p^2,\sigma _e^2} \right) \propto {\left( {\sigma _e^2} \right)^{ - {1 \over 2}N}}{\mkern 1mu} \exp \left( { - {1 \over 2}{{\left( {y - Xb - {Z_a}a - {Z_p}p} \right)}^\prime }\left( {y - Xb - {Z_a}a - {Z_p}p} \right)/\sigma _e^2} \right)$$
$${\rm{X}}\Delta {\left( {\sigma _a^2} \right)^ - }^{{1 \over 2}{N_a}}\exp \left( { - {1 \over 2}{{{\rm{a'}}}_1}{{\rm{A}}^{ - 1}}{a_1}/\sigma _a^2} \right)\left[ {\prod\limits_{t = 2}^T {{{\left( {\sigma _a^2} \right)}^{ - {1 \over 2}{N_a}}}} \exp \left( { - {1 \over 2}{{\left( {{{\rm{a}}_{\rm{t}}} - {{\rm{a}}_{{\rm{t}} - 1}}} \right)}^\prime }{{\rm{A}}^{ - 1}}\left( {{{\rm{a}}_{\rm{t}}} - {{\rm{a}}_{{\rm{t}} - 1}}} \right)/\sigma _a^2} \right)} \right]$$
$${\rm{X}}\Delta {\left( {\sigma _p^2} \right)^{ - {1 \over 2}{N_p}}}\exp \left( { - {1 \over 2}{{{\rm{p'}}}_1}{{\rm{p}}_1}/\sigma _e^2} \right)\left[ {\prod\limits_{t = 2}^T {{{\left( {\sigma _p^2} \right)}^{ - {1 \over 2}{N_p}}}} \exp \left( { - {1 \over 2}{{\left( {{{\rm{p}}_{\rm{t}}} - {{\rm{p}}_{{\rm{t}} - 1}}} \right)}^\prime }{{\rm{I}}^{ - 1}}\left( {{{\rm{p}}_{\rm{t}}} - {{\rm{p}}_{{\rm{t}} - 1}}} \right)/\sigma _p^2} \right)} \right]$$
$${\rm{X}}{\left( {\sigma _e^2} \right)^{ - \left( {{{{\nu _e}} \over 2} + 1} \right)}}\exp \left[ { - {{{\nu _e}{S_e}} \over {2\sigma _e^2}}} \right]{\left( {\sigma _a^2} \right)^ - }^{\left( {{{{\nu _a}} \over 2} + 1} \right)}\exp \left[ { - {{{\nu _a}{S_a}} \over {2\sigma _a^2}}} \right]{\left( {\sigma _p^2} \right)^{ - \left( {{{\nu p} \over 2} + 1} \right)}}\exp \left[ { - {{{\nu _p}{S_p}} \over {2\sigma _p^2}}} \right]...................(3)$$
Last line of (3) are product of density of scaled inverted chi-square distributions assumed prior for variance parameters. ∆ is assumed to be 1 for random walk model. After algebraic manipulations conditional distributions could be written as following,
$${b_t}\left| {\sigma _a^2,\sigma _p^2,\sigma _e^2,{a_t},{p_t},{y_t} \sim N\left( {{{\left( {X'X} \right)}^{ - 1}}X'\left( {y - {Z_a}a - {Z_p}{p_t}} \right),{{\left( {X'X} \right)}^{ - 1}}\sigma _e^2} \right)} \right.$$
$${a_t}\left| {\sigma _a^2,\sigma _p^2,\sigma _e^2,{b_t},{p_t},{y_t}} \right. \sim $$
$$N\left( {{{\left( {{1 \over {\sigma _e^2}}{{{\rm{Z'}}}_{{a_t}}}{{\rm{Z}}_{{a_t}}} + {2 \over {\sigma _a^2}}{{\rm{A}}^{ - 1}}} \right)}^{ - 1}}\left( {{1 \over {\sigma _e^2}}{\rm{Z'}}\left( {{{\rm{y}}_t} - {{\rm{X}}_{\rm{a}}}{{\rm{b}}_t} - {{\rm{Z}}_{{{\rm{p}}_{\rm{t}}}}}{{\rm{p}}_{\rm{t}}}} \right) + {1 \over {\sigma _a^2}}{{\rm{A}}^{ - 1}}{a_{t + 1}}} \right),{{\left( {{1 \over {\sigma _e^2}}{{{\rm{Z'}}}_{{{\rm{a}}_{\rm{t}}}}}{{\rm{Z}}_{{{\rm{a}}_{\rm{t}}}}} + {2 \over {\sigma _a^2}}{{\rm{A}}^{ - 1}}} \right)}^{ - 1}}} \right)$$
$${p_t}\left| {\sigma _a^2,\sigma _p^2,\sigma _e^2,{a_t},{b_t},{y_t}} \right. \sim $$
$$N\left( {{{\left( {{1 \over {\sigma _e^2}}{{{\rm{Z'}}}_{{p_t}}}{{\rm{Z}}_{{p_t}}} + {2 \over {\sigma _p^2}}{{\rm{I}}^{ - 1}}} \right)}^{ - 1}}\left( {{1 \over {\sigma _e^2}}{\rm{Z'}}\left( {{{\rm{y}}_t} - {{\rm{X}}_{\rm{a}}}{{\rm{b}}_t} - {{\rm{Z}}_{{{\rm{p}}_{\rm{t}}}}}{{\rm{a}}_{\rm{t}}}} \right) + {1 \over {\sigma _p^2}}{{\rm{I}}^{ - 1}}{a_{t + 1}}} \right),{{\left( {{1 \over {\sigma _e^2}}{{{\rm{Z'}}}_{{{\rm{p}}_{\rm{t}}}}}{{\rm{Z}}_{{{\rm{p}}_{\rm{t}}}}} + {2 \over {\sigma _p^2}}{{\rm{I}}^{ - 1}}} \right)}^{ - 1}}} \right)$$
$$\sigma _a^2\left| {\sigma _p^2,\sigma _e^2,{p_t},{a_t},} \right.{b_t},{y_t} \sim {{\left( {{Q_a} + {\nu _a}{S_a}} \right)} \over {\chi _{DF}^2}}$$
$$\sigma _p^2\left| {\sigma _a^2,\sigma _e^2,{p_t},{a_t},} \right.{b_t},{y_t} \sim {{\left( {{Q_p} + {\nu _p}{S_p}} \right)} \over {\chi _{DF}^2}}$$
$$\sigma _e^2\left| {\sigma _a^2,\sigma _p^2,{p_t},{a_t},} \right.{b_t},{y_t} \sim {{\left( {{Q_e} + {\nu _e}{S_e}} \right)} \over {\chi _{DF}^2}}$$
where in the last two line Qa , Qp and Qe stands for quadratic form of the respective error terms and DF degrees of freedoms. We ran the model with 10,000 iterations using a 5000-iteration burn-in period for DBP. To reduce auto-correlation, we sampled every tenth iteration. We tried different parameters of inverse Wishart prior distributions to obtain residuals.
We used a mixed model to perform genome-wide association analyses [9,7] using R software [10]:
$${\rm{y = }}\,{\rm{Xb}}\,{\rm{ + }}\,{\rm{e}}..........{\rm{(4)}}$$
where y contains the residuals or random effects from (3), b designates the fixed effects (SNP), X and is incidence $$matrices,and\,e\,is\,a\,vector\,containing\,residuals\,\,and\,assumed\,normally\,distributed\,with\,I\,\sigma _e^2.\,I\,is\,an\,identity\,matrix,\sigma _e^2$$ is the residual variance. We used a false discovery threshold of 5 % to detect a genomic signal in association mapping. We also used cross sectional GRAMMAR [1] approach by each time points for comparison purposes. We estimated heritability of DBP as 0.299 and 0.259 using genomic coancestry matrix [9] and pedigree information respectively.
Analyses were performed without knowledge of the underlying simulation model. However, we used the GAW18 answers in discussing the results.
We confirmed the normality using Kolmogrow-Smirnov test. However since we employed Bayesian residuals: all response variables transformed to be normally distributed (P > 0.01). Time, Sex, smoking status, age and pedigree number was included as a fixed effect in subsequent analyses based on preliminary analyses using correlations between predictions and observations. We found that correlations between predictions and observations were highest up to 0.15. Error, genetic and permanent environmental variance components were predicted as 17.3 (0.0006), 10.9 (0.0007) and 8.2 (0.0006) using genomic relation matrix and 18.0 (0.0007), 9.2 (0.0008) and 8.4(0.0006) using pedigree relation matrix for DBP. DBP was simulated with 0.317 heritability whereas genomic kinship estimates were found to be closer to its true value (Tables 1-3).
Assumptions regarding evolution of gene and permanent environmental effects over time might be important. Certain degree of autoregressive structure might be more realistic compared with a random walk model. We simply tuned the model based on restrictions of parameters space in (3) using ∆ . We considered two extreme cases for deviation from random walk using ∆=0.1 and ∆=0.9. Random walk assumes that gene effects could change slowly in both up and down directions over time, ∆=1.0,. Autoregressive structure for both gene and environmental effects could be introduced by tuning ∆ to obtain stationary distributions. Here the time series will be distributed around the mean trajectory.
Error, genetic and permanent environmental variance components were predicted as 10.26 (0.0006), 1.98 (0.0001) and 1.98 (0.0003) using ∆=0.1 and 14.2 (0.0002), 6.4 (0.0009) and 5.5 (0.0006) using ∆=0.9 for DBP. Heritability were predicted as 0.299, 0.139 and 0.246 using ∆=1.0, ∆=0.1 and ∆=0.9 .The random walk gave better results compared with autoregressive structures (DBP was simulated with 0.317). We hypothesis that: increasing the time points should decrease the genomic inflation factors [7] due to accumulation of information regarding both relatedness and substructure over time. We employed both genomic and pedigree based relationship matrix in the mixed model (3). Genomic relationship matrix found to give lower genomic inflation factor as 1.40, 1.33, and 1.63 compared with pedigree based relationship matrix 1.57, 1.83, and 1.59 over three time points for DBP. Due to small number of time points (t=3) still we obtained high level of genomic inflation factors ( λ > 1 ). Table 1 and Table 2 shows that both genomic relationship and pedigree relationship matrix detected mostly different set of SNPs for different time points.
However both small sampling size and small number of time points may lead to false positives and false negatives. This may be true especially for very first time point: genomic relationship matrix detected 154 SNPs at 5 % False Discovery Rate (FDR) (134 and 56 SNPs detected for time points 2 and 3 respectively at 5 % FDR) and pedigree relationship matrix detected 216 SNPs at 5 % FDR (300 and 96 SNPs detected for time points 2 and 3 respectively at 5 % FDR). Due to smaller genomic inflation factors we investigated results of genomic relationship matrix for causal SNPs. rs11711953 from time point 1, 2 and 3 is found to be associated with MAP4 gene.
We used GRAMMAR approach to analyze each time points (and average of them) cross sectionally (Table 3). However we did not detect any genomic signals after multiple hypothesis corrections. Although there was signals from time point 2 by rs1948722 at the vicinity of ARHGEF3 (p<0.00012), the SNP became non significant after multiple hypothesis correction by FDR. Magnitude of GRAMMAR p values (Table 3) found to be larger compared with the p values of random walk models (Tables 1,2). This clearly shows that longitudinal gene and environmental effects over time needs to be taken into account by proper methodology. Otherwise since the genomic signals will be contaminated by stochastic errors this may lead to either undetection of the signals or may also lead to false positives. Random walk is a non stationary process and in this paper we extended the model for stationary case by tuning ∆ parameter. However theoretical and empirical dynamic association studies are needed if non stationary assumption is useful or not for dynamics of gene and permanent environmental effects.
Genomic relationship matrix gave better inflation factors and estimates of heritability compared with pedigree information. The random walk model may be useful for long time series in practice due to its recursive structure from Kalman filter. When the longitudinal observations available (daily or monthly for example) the model could predict the on-line genomic signals sequentially due to the Kalman Filter. In genomic studies failing to taken into account of longitudinal gene and environmental effects over time may lead to either undetection of true signals and/ or may also lead to false positives due to stochastic errors.
The Genetic Analysis Workshops are supported by National Institutes of Health (NIH) grant R01 GM031575 from the National Institute of General Medical Sciences. This work was supported by Research Fund of the Akdeniz University Project Number 106. The author wishes to acknowledge useful discussions with Dr Luc Janss about auto regressive structures.

Table 1: Top 10 SNPs and correspondent raw p values obtained using random walk model from genomic relationship matrix for first replicate of DBP
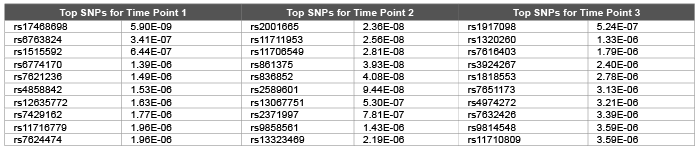
Table 2: Top 10 SNPs and correspondent raw p values obtained using random walk model from pedigree relationship matrix for first replicate of DBP
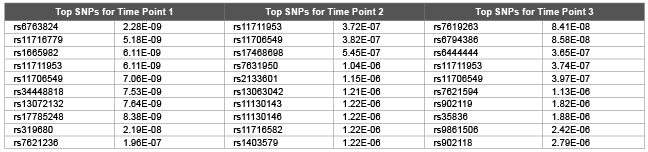
Table 3: Top 10 SNPs and correspondent raw p values obtained using GRAMMAR for first replicate of DBP
There are no competing interests.
Download Provisional PDF Here
Aritcle Type: Research Article
Citation: Karacaören B (2015) Dynamic Association Mapping based on a Kalman Filter Model using GAW 18 Data Set. Int J Mol Genet Gene Ther 1 (1): http://dx.doi.org/10.16966/2471-4968.101
Copyright:© 2015 Karacaören B. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
All Sci Forschen Journals are Open Access