
Full Text
Yi Wang Jiajia Xie Xun Liu Jielin Du Mingyue Wu Wenjing Huang Dan Deng*
Department of Health Statistics, School of Public Health and Management, Chongqing Medical University, China*Corresponding author: Dan Deng, Department of Health Statistics, School of Public Health and Management, Chongqing Medical University, 1 Yixueyuan Road, Yuzhong District, Chongqing 400016, China, E-mail: 100079@cqmu.edu.cn
Objectives: To compare the ability of logistic regression and generalized boosted modelling (GBM) to estimate treatment effects and balance covariates in inverse probability of treatment weighting (IPTW) and to explore the independent impact of different types of medical insurance on drug costs of outpatients with coronary heart disease based on this method.
Methods: This study was used to evaluate the performance of logistic regression and GBM in IPTW under a Monte Carlo study with the simulated design of linear and nonlinear correlations between treatment variable and covariates of different sample sizes (n=500, 2000). The assessment indicators included average standardized absolute mean difference (ASAM), point estimation, bias, relative bias, standard error, mean square error, 95% confidence interval coverage rate, distribution of weights and an empirical study of outpatients with coronary heart disease was carried out after simulation.
Results: The simulations show that GBM in propensity score weighting is superior to logistic regression in the lower bias and mean square error and it achieves better covariate balance, especially in nonlinear conditioning models. And in this case study. It’s found that GBM in IPTW has better ability to balance the confounding factors compared with logistic regression. The weighted results show that the drug costs of outpatients with coronary heart disease of Urban Employee Basic Medical Insurance increase by 256.35 Yuan on average compared with those of Urban-Rural Resident Basic Medical Insurance.
Conclusion: It may be better to control confounding factors in case of the unknown relationship between the treatment variable and covariates by IPTW with GBM. There is still a certain gap in drug costs among different types of medical insurance for patients with coronary heart disease according to this study, which provides a reasonable scientific basis for the optimal allocation of medical insurance system and health resources in coronary heart disease.
Propensity score; Inverse probability of treatment weighting; Generalized boosted modelling; Simulation; Coronary heart disease
Although randomized controlled trials are regarded as the gold standard in research design, they are often not implemented or cannot accurately reflect the effect of interest in real experimental designs or social and health sciences due to ethics, time and cost constraints and other reasons [1,2]. A large quantity of observational data has become easily available with the development of hospital informatization. However, observational studies cannot control the confounding factors between treatment and non-treatment groups by means of random assignment. Therefore, selection bias often occurs when estimating the treatment effect. Traditional methods used to reduce bias in observational studies include regression models, matching and stratification, but these methods may not be suitable for studies with a large number of covariates [3-5]. Propensity score methods can transform multiple covariates (multi-dimensional) into propensity scores (one-dimensional), which can solve these problems. The application of propensity score methods includes mainly matching, stratification, weighting and regression adjustment [6-9]. Propensity score weighting has substantial advantages over matching and is used to analyse treatment effects by retaining all the individuals in the sample, which can significantly improve statistical efficiency. In recent years, propensity score weighting has been increasingly being used in the medical field [10-12].
Propensity scores are commonly estimated by logistic regression [13-15]. Modelling requires several assumptions related to selecting variables and specifying functional forms [16-18]. Therefore, subjective decisions are often involved in finding the best model. Moreover, when one of these assumptions is wrong, covariate balance may be impossible to achieve by adjusting propensity scores, which may lead to bias in the estimation of the treatment effect [19,20]. In addition, logistic regression cannot address complex relationships such as non linear and interaction effects between covariates [21-23]. Generalized boosted modelling (GBM), one of the latest prediction methods in machine learning, is superior to logistic regression in addressing high-dimensional and missing data [1,24,25] and can be used as an alternative nonparametric method to achieve the same purpose but with fewer assumptions and more accurate results. Unfortunately, GBM is not widely used with propensity scores. Therefore, in the absence of hidden bias and different sample sizes, this study intends to construct linear and nonlinear conditioning models to compare the ability of logistic regression and GBM to estimate the treatment effect and balance covariates in propensity score weighting to provide some reference for the processing of confounding factors of various complex data. In Chongqing, Coronary heart disease (CHD) was included in special disease management in 2012. The reimbursement rates of different types of medical insurance are different [26,27], so we wanted to analyse the independent impact of medical insurance between urban employees and urban-rural residents on drug costs of outpatients with CHD. However, because of the large sample size of outpatient data and the uneven baseline, we used this case study as an empirical analysis.
Basic assumptions and the average treatment effect
As proposed originally by Rosenbaum PR, et al. [28], the propensity score refers to the conditional probability that membersi (i=1,...,N) were assigned to a particular treatment group (W=1) rather than non-treatment group (W =0) given the observed covariate vector where e(X) is also called a balancing score and X is a vector e(X)=pr(W=1│X), of observed baseline covariates that may impact the selection of the treatment and outcome variables. Treatment assignments are independent of the observed baseline covariates given the propensity score X⊥W│e(X) . Therefore, if the propensity scores of the treatment and non-treatment groups are similar, each member has the same probability of being assigned to the treatment group as in a randomized experiment, even though they have different values of some covariates. If the strongly ignorable treatment assumption (SITA) is achieved, that is, the potential outcomes of the treatment (Y1) and non-treatment (Y0) groups are independent of the selection of treatment (Y0,Y1)⊥W│X, then an unbiased estimate of the average treatment effect (ATE) is written as ATE=E[Y1│W=1)-(Y0│W=0)│X. Propensity score weighting aims to assign a weight to every member such that the weights represent the whole. The method of estimating ATE is known as the inverse probability of treatment weighting (IPTW). The weight for the treatment group is 1/ e(X ) and for the non-treatment group is 1/(1-e(X)). Instead of creating similar propensity between two groups, IPTW creates a weighted analysis with unequal weights, which is easy to implement. Therefore, if propensity scores are properly estimated, the weights can explain the difference in the observed covariate distribution between the treatment and non-treatment groups, and ATE is equal to the weighted average of the difference between the outcomes of the two groups, that is,
When e(Xi) is estimated by machine learning, no explicit formula may exist for variance estimation. To show the weights more clearly, Imbens GW [30] proposed an alternative standardized estimator for ATE, which is written as
The conditioning model for predicting propensity scores
Logistic regression: The process of obtaining propensity scores with logistic regression is very simple and easy to understand and perform, but the model must be transformed into a linear model via an appropriate connection function such as the logit function [31]. However, when the relationship between covariates and transformation variables does not satisfy the linear hypothesis, the values of the propensity scores are often unreliable.
Generalized boosted modelling: GBM is a modern nonparametric boosting method based on a regression tree that can fit multiple models with a regression tree as a weak classifier and then use a boosting algorithm to merge the predictions from each model [32,33]. Regression trees can be applied to continuous, normal, ordered and missing independent variables to automatically obtain nonlinear relations and interactions [34]. In contrast to logistic regression, there is no need to set the functional form of the predictive variable. The boosting algorithm can combine many simple models into a more complex model. Compared with a simple regression tree, the boosting algorithm can obtain smooth fitting and good prediction and to a large extent, can avoid over fitting the data [35,36]. Thus, GBM is used to incorporate a large number of measured baseline covariates to fit a conditioning model. The formula for estimating a propensity score is g(X)= logit(e(X))-log(e(X)/(1-e(X))) [37]. Specifically, GBM begins with a regression tree and sets ĝ0(X)=logw/(1-w) as the initial value, where w is the mean of the treatment variable in the sample. Then, an adjustment function h(X) is found to improve the fitting degree of the model. h(X) can be in any form: here, it is the regression tree obtained by fitting the residuals of the currently estimated logit(e(X)) with X. logit(e(X)) is updated by gˆ(X ) + λh(X ) by means of continuous iteration, and the estimation of the loglikelihood increases correspondingly with every iteration. λ is a shrinkage coefficient: generally, the smaller λ is, the smoother the fit is. The shrinkage coefficient ranges from 0 to 1. McCaffrey suggested stopping the number of iterations when the average standardized absolute mean difference (ASAM) on measured baseline covariates is minimized [37]. In this study, the shrinkage coefficient is 0.01, and the stopping rule is to minimize the ASAM across covariates.
Simulation design
The simulated structure described by Shenyang Guo and Mark W. Fraser in the book named “Propensity Score Analysis: Statistics Methods and Applications” was modified slightly in this study [1]. First, five baseline covariates ( X1−X5) were considered X1, X3 and X5 were continuous variables that followed a normal distribution with a mean vector (3 11 6) and standard deviation vector (0.3 4.0 2.5), and X2 and X4 were classified variables of a Bernoulli distribution. A binary treatment variable with two groups of treatment exposure was created, three variables ( X1, X2, and X5 ) were used to generate the treatment variable (W ), and the probability of the treatment assignment for each group was defined as Pr(W=1│Xi)=1/(1+exp(-(f(Xi,β)+v))). Function f changed with the variation of coefficient β in different situations, and the average treatment probability was approximately 0.5. Variables X1 to X4 were used to compute a continuous outcome variable (Y ) from the following regression equation: Y=α0+ αiXi+τW+u. The true treatment effect (τ ) was equal to 1.5, which was known in advance. The error terms for the treatment ( v ) and outcome (u ) variables, which represented the amount of unexplained variance after accounting for independent variables, were both generated from normal distributions with mean 0 and variance 1. According to SITA, when X5 was correlated with the outcome error (u ) but the treatment error ( v ) and outcome error (u ) were uncorrelated, no hidden bias existed in specifying the conditioning model. The correlation coefficients for distinct pairs of variables among X1, X3, and X5 and u were 0.2(rX1X3), 0.15(rX3X5) and 0.5(ruX5) and the relationships among the other variables were set to zero. Weak relationships among the variables ( X1− X5) were considered to reduce potential variability in the simulated data. In this study, two scenarios were considered to estimate ATE using IPTW, and propensity scores were estimated using logistic regression and GBM. The two scenarios were as follows:
Scenario 1: The relationship between the treatment variable and baseline covariates was linear, that is, the correct conditional model for predicting propensity scores was W=[ β0+ β1X3+ β2X4+ β3X5+v], and the outcome regression model was Y=[ α0+ α1X1+ α 2X2+α3X3+ α4X4 +αWW+u].
Scenario 2: The relationship between the treatment variable and baseline covariates was nonlinear. Additionally, there were no interaction effects and quadratic terms, that is, the correct conditional model for predicting propensity scores was W=[ β0+ β1X3+ β2X4+ β3X5+ β4X23+ β5X3X5+ β6X3X4+v], and the outcome regression model was Y=[ α0+ α1X1+ α 2X2+α3X3+ α4X4 +αWW+u]. Here, α0=100,αi=(0.7, 0.25, -0.4, 0.15), and βi =(0, -0.28, 0.15, 0.5, -0.042, 0.09, -0.056). Both scenarios were simulated with 1000 datasets of sample sizes N=500 and N=2000.
Statistical analysis
All analyses were conducted in the R software environment (version 3.5.3) and STATA (version 15.0). IPTW with GBM was implemented using the ps function from the twang package, and IPTW with logistic regression was implemented using the dxwts function. All other analyses were conducted in STATA. The following were used as metrics to assess the different conditioning models:
Average standardized absolute mean difference: used to test the balance of baseline covariates, a low ASAM indicates that specific values of baseline covariates between two groups are similar; The performance of estimated treatment effects: point estimation (αW), bias, relative bias (RB) and standard error of the effect estimation (SE); Mean Square Error (MSE): the variation in the sampling distribution of estimated treatment effects, a smaller value indicates higher model accuracy and less variation; 95% CI coverage rate: the percentage of the 95% confidence interval estimated by the model containing the true treatment effect; Distribution of weights: propensity scores range from 0 to 1. Values close to 0 or 1 entail extreme weights that reduce the accuracy of IPTW.
All indicators were calculated as the average of 1000 results.
Simulation results
The treatment effect and accuracy of the models: When the conditioning model was linear, the RB of logistic regression (N=500:0.20%, N=2000:0.17%) was slightly lower than that of GBM (N=500:0.28%, N=2000:0.27%). The average standard error, MSE and 95% CI coverage rate were similar, and the standard error and MSE decreased with increasing sample size, while the 95% CI coverage rate decreased with increasing sample size. When the conditioning model was nonlinear, the RB of logistic regression (N=500:0.55%, N=2000:0.77%) increased significantly, and many outliers were observed in the distribution of bias, while GBM remained stable (N=2000:0.37%). The average standard error (N=500:0.1401, N=2000:0.0909) and MSE (N=500:0.0428, N=2000:0.0175) of logistic regression increased significantly and were higher than those of GBM under the same sample size. The 95% CI coverage rate (N=500:81.7%, N=2000:82.7%) decreased significantly and was lower than that of GBM. The larger the sample size was, the better the results were (Table 1 and Figure 1).
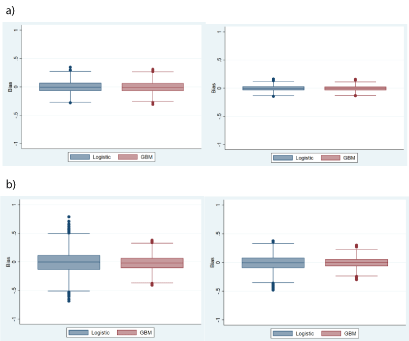
Figure 1:
a: Distribution of bias with sample sizes of 500 (left) and 2000 (right) by two methods in scenario 1.
b: Distribution of bias with sample sizes of 500 (left) and 2000 (right) by two methods in scenario 2.
| Sample size | Method | αW | SE | Bias | RB | MSE | 95% CI coverage rate | ASAM | |
| Scenario 1 | N=500 | Logistic | 1.4970 | 0.0950 | 0.0030 | 0.20% | 0.0103 | 93.2% | 0.048 |
| GBM | 1.4958 | 0.0950 | 0.0042 | 0.28% | 0.0100 | 93.5% | 0.121 | ||
| N=2000 | Logistic | 1.4975 | 0.0484 | 0.0025 | 0.17% | 0.0023 | 93.9% | 0.025 | |
| GBM | 1.4960 | 0.0475 | 0.0040 | 0.27% | 0.0022 | 94.9% | 0.073 | ||
| Scenario 2 | N=500 | Logistic | 1.4918 | 0.1401 | 0.0082 | 0.55% | 0.0428 | 81.7% | 0.738 |
| GBM | 1.4786 | 0.1297 | 0.0214 | 1.43% | 0.0199 | 92.9% | 0.273 | ||
| N=2000 | Logistic | 1.4884 | 0.0909 | 0.0116 | 0.77% | 0.0175 | 82.7% | 0.452 | |
| GBM | 1.4944 | 0.0808 | 0.0056 | 0.37% | 0.0077 | 92.9% | 0.195 |
Table 1: The results of IPTW with logistic regression and GBM under two scenarios.
The balance of baseline covariates: The distribution of ASAM in the original sample was highly imbalanced between the two groups (scenario 1: average ASAM>0.2; scenario 2: average ASAM>0.4). When the conditioning model was linear, balanced baseline covariates could be achieved. Compared with GBM, the average ASAM of logistic regression was low (N=500:0.048, N=2000:0.025). When the conditioning model was nonlinear, the ability to achieve covariate balance based on GBM was better than that of logistic regression, and the average ASAM of logistic regression (N=500:0.738, N=2000: 0.452) increased significantly, even higher than in the original sample (N=500:0.421, N=2000:0.273). In addition, logistic regression had a large number of high outliers in both scenarios (Table 1 and Figure 2).
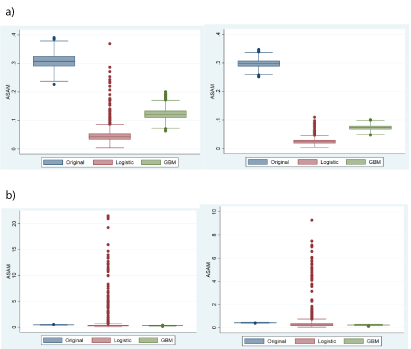
Figure 2:
a: Distribution of ASAM with sample sizes of 500 (left) and 2000 (right) by two methods in scenario 1.
b: Distribution of ASAM with sample sizes of 500 (left) and 2000 (right) by two methods in scenario 2.
Distribution of weights: When the conditioning model was linear, the distributions of weights by logistic regression and GBM were similar under the same sample size, all of which are centred on 1. When the conditioning model was nonlinear, logistic regression generated a large number of extremely high weights under different sample sizes. The average weights were 22.07 and 5.79, and the average maximum weights were 10126.87 and 7462.96, respectively. By contrast, the weights generated by GBM remained stable. The average weights were 1.45 and 1.56, and the average maximum weights were 16.17 and 44.09, respectively (Table 2).
| Sample size | Method | Distribution of weights | ||||||
| Min | P25 | P50 | Mean | P75 | Max | |||
| Scenario 1 | N=500 | Logistic | 1.01 | 1.24 | 1.53 | 1.99 | 2.12 | 20.2 |
| GBM | 1.02 | 1.21 | 1.43 | 1.74 | 1.90 | 8.67 | ||
| N=2000 | Logistic | 1.01 | 1.25 | 1.54 | 2.00 | 2.14 | 32.55 | |
| GBM | 1.02 | 1.23 | 1.47 | 1.85 | 2.02 | 13.63 | ||
| Scenario 2 | N=500 | Logistic | 1.00 | 1.02 | 1.11 | 22.07 | 1.46 | 10126.87 |
| GBM | 1.00 | 1.04 | 1.12 | 1.45 | 1.38 | 16.17 | ||
| N=2000 | Logistic | 1.00 | 1.02 | 1.10 | 5.79 | 1.44 | 7462.96 | |
| GBM | 1.00 | 1.03 | 1.10 | 1.56 | 1.38 | 44.09 | ||
Table 2: Distribution of weights by IPTW with logistic regression and GBM under two scenarios.
Case study
Outpatient data of patients with CHD were selected to examine the performance of IPTW with the different methods for estimating ATE. The outpatient data from a tier-3 hospital in Chongqing collected from January 2016 to December 2018 consisted of demographic information and drug costs of patients. Inclusion criteria: hospital admissions of CHD were identified based on the first diagnosis with International Classification of Diseases 10th revision (ICD-10) codes of I20-I25. Exclusion criteria: combination of other diseases. The study was intended to analyse the independent impact of different types of medical insurance on drug costs in outpatients with CHD, because the cost is also affected by other demographic factors, so propensity score weighting is used to control other confounding factors. The outcome variables of this study were the drug costs of outpatients with CHD, exposure variables were different types of medical insurance, potential confounding factors included gender, age, category of drug, drug’s zero-profit policy doctor’s title and type of department and 16575 people were included, of which 15136 were ensured with Urban Employee Basic Medical Insurance (UEBMI) and 1439 with UrbanRural Resident Basic Medical Insurance (URRBMI).
Balance of covariates and weights: Before weighting, the maximum and average ASAM were 0.393 and 0.179, respectively. The other variables, except the category of drug, varied between the two groups (P<0.05). After IPTW with logistic regression, the maximum and average ASAM were 0.090 and 0.030, respectively. The average weight was 2.00, and the category of drugs and drug’s zero-profit policy were different between the two groups (P<0.05). After IPTW with GBM, the maximum and average ASAM were 0.081and 0.027, respectively. The average weights were 1.95, and no difference in any variables between the two groups was observed (P>0.05) (Table 3). GBM performed better than logistic regression, so IPTW with GBM was used in the subsequent analysis.
| Covariates | Unweighting | IPTW with logistic regression | IPTW with GBM | ||||||||||
| UEBMI (n=15136) | URRBMI (n=1439) | ASAM | P | UEBMI (n=15136) | URRBMI (n=1439) | ASAM | P | UEBMI (n=15136) | URRBMI (n=1439) | ASAM | P | ||
| Gender | Male | 62.1% | 57.1% | 0.103 | <0.001 | 61.7% | 62.2% | 0.010 | 0.782 | 60.7% | 60.6% | 0.023 | 0.577 |
| Female | 37.9% | 42.9% | 0.103 | 38.3% | 37.8% | 0.010 | 38.3% | 39.4% | 0.023 | ||||
| Category of drug | Western Medicine | 93.7% | 93.3% | 0.016 | 0.570 | 93.7% | 95.7% | 0.090 | 0.018 | 93.7% | 93.7% | 0.002 | 0.980 |
| Non-Western Medicine | 6.3% | 6.7% | 0.016 | 6.3% | 4.3% | 0.090 | 6.3% | 6.3% | 0.003 | ||||
| Drug’s zero- profit policy | Before | 58.8% | 74.5% | 0.321 | <0.001 | 60.1% | 64.3% | 0.086 | 0.020 | 60.1% | 63.4% | 0.066 | 0.103 |
| After | 41.2% | 25.5% | 0.321 | 39.9% | 35.7% | 0.086 | 39.9% | 36.6% | 0.066 | ||||
| Doctor’s title | primary | 4.4% | 2.2% | 0.105 | <0.001 | 4.2% | 3.8% | 0.017 | 0.343 | 4.2% | 3.2% | 0.051 | 0.491 |
| intermediate | 21.2% | 15.9% | 0.129 | 20.7% | 23.4% | 0.066 | 20.7% | 21.6% | 0.022 | ||||
| Deputy senior | 34.5% | 28.0% | 0.136 | 33.9% | 31.2% | 0.057 | 33.9% | 32.4% | 0.033 | ||||
| Senior | 40.0% | 53.9% | 0.283 | 41.2% | 41.6% | 0.008 | 41.2% | 42.9% | 0.034 | ||||
| Type of department | The others | 3.0% | 5.2% | 0.128 | <0.001 | 3.2% | 3.2% | 0.001 | 0.812 | 3.2% | 3.4% | 0.013 | 0.554 |
| Endocrinology and Metabolism | 3.2% | 0.4% | 0.157 | 2.9% | 2.1% | 0.047 | 2.9% | 1.6% | 0.081 | ||||
| General internal medicine | 5.5% | 3.9% | 0.069 | 5.3% | 4.7% | 0.025 | 5.3% | 5.4% | 0.003 | ||||
| TCM -WM | 14.8% | 2.6% | 0.345 | 13.8% | 15.0% | 0.036 | 13.8% | 13.1% | 0.019 | ||||
| Cardiovascular | 66.1% | 84.7% | 0.393 | 67.7% | 67.9% | 0.004 | 67.7% | 70.1% | 0.051 | ||||
| Geriatrics | 7.4% | 3.2% | 0.162 | 7.1% | 7.0% | 0.004 | 7.1% | 6.4% | 0.025 | ||||
| Age(year) | 0~ | 1.8% | 6.3% | 0.033 | <0.001 | 2.2% | 2.2% | 0.001 | 0.740 | 2.2% | 2.2% | 0.003 | 0.926 |
| 45~59 | 16.1% | 22.0% | 0.159 | 16.6% | 15.5% | 0.031 | 16.6% | 16.0% | 0.018 | ||||
| 60~74 | 56.8% | 47.0% | 0.197 | 55.9% | 56.7% | 0.016 | 55.9% | 56.2% | 0.006 | ||||
| 75~ | 25.3% | 24.7% | 0.012 | 25.2% | 25.7% | 0.009 | 25.2% | 25.6% | 0.008 | ||||
| Maximum ASAM | 0.393 | 0.090 | 0.081 | ||||||||||
| Average ASAM | 0.179 | 0.030 | 0.027 | ||||||||||
| Average weights | - | 2.000 | 1.950 | ||||||||||
Table 3: ASAM and P values in covariates of two groups before and after weighting.
Estimation of ATE: After weighting, the drug costs of outpatients with UEBMI increased by 256.35 Yuan on average compared with those of outpatients with URRBMI. The difference was statistically significant (Table 4).
| IPTW with GBM | ||||
| β(se) | t | P | 95% CI | |
| Types of medical insurance |
256.35(16.17) | 15.86 | <0.001 | 224.66-288.04 |
Table 4: Estimation of ATE after IPTW with GBM.
Sensitivity analysis: For sensitivity analysis, we repeated the analyses after excluding patients in the tails of the distribution of propensity scores [38]. And the conclusions were consistent with those of the primary analyses (Table 5).
| PS Trimming Range | IPTW with GBM | |||
| β(se) | t | P | 95% CI | |
| 1%-99% | 256.44(16.42) | 15.62 | <0.001 | 224.25-288.62 |
| 2.5%-97.5% | 255.38(17.02) | 15.00 | <0.001 | 222.02-288.74 |
| 5%-95% | 255.87(17.62) | 14.52 | <0.001 | 221.32-290.41 |
Table 5: Sensitivity Analysis for Estimation of ATE after IPTW with GBM.
The main objective of IPTW is to achieve covariate balance between treatment and non-treatment groups to obtain an effective estimation of the treatment effect. Most methods use logistic regression to predict propensity scores, but the model assumptions may not be valid. Therefore, the main purpose of this study is to compare the ability of logistic regression and GBM to estimate the treatment effect and covariate balance in propensity score weighting under linear or nonlinear conditioning models. Although Jacqueline M Burgette, et al., Xin M, Fullerton B and other researchers [39-41] compared logistic regression with GBM, they did not consider the interaction effect and quadratic relationships among the treatment variable and covariates. Moreover, this study assessed the covariate balance and distribution of weights to make the results more reliable. In addition, the design ensured that no hidden bias existed in estimating the conditioning model, that is, the source of the difference between the two groups could be determined and propensity score weighting could be used to control the bias.
The results showed that both logistic regression with only main effects and GBM usually achieved covariate balance and provided acceptable estimation of treatment effects, regardless of sample size. The distribution of weights was centralized with 1 as the centre, the 95% CI coverage rate was close to 95%, and the accuracies of the models were similar. Abdia Y, et al., Pirracchio R, et al. [42,43] also noted that logistic regression produced lower ASAM and smaller bias than did machine learning under a linear model. However, when the model did not consider the interaction effect and quadratic terms, regardless of sample size, the ASAM values estimated by logistic regression were higher than those of the unweighted values. Moreover, the skewed distribution produced a large number of high outliers and failed to achieve balanced covariates. These results were similar to those observed by Abdia Y, et al., Lee BK, et al. and his colleagues [42,44], where the estimated weights were highly scattered. For example, when N=2000, the range was from 1 to 7462.96. The main reason may be that the degree of overlap on covariates between two groups is not high, and only a few members of any group can replace other members in the other group. Another study showed that if the estimated weights are highly variable, the weights might lead to poor accuracy of the ATE [45-48]. The bias in this scenario was approximately 3 times larger than that in the linear scenario, the standard error was approximately 2 times larger, the MSE was approximately 8 times larger, and the 95% CI coverage rate was reduced by 10%. By contrast, the ASAM estimated by GBM remained steady and had a more symmetrical distribution. GBM provided good performance in terms of covariate balance. The weight distribution remained stable (e.g., when N=500, the range was from 1 to 16.17), the 95% CI coverage rate was still greater than 90%, and other indicators were slightly worse. However, the performance of these indicators was better when N=2000, possibly because machine learning itself was more suitable for larger sample sizes. In addition, when the nonlinear relationship between covariates in the conditioning model was excessively complex, the logistic regression model could not be fitted. These results indicate that it may be important to balance covariates with interaction effects and quadratic terms, especially when the real model itself has interaction effects and quadratic terms. Alam S, et al., Franklin JM, et al., Lunt M and others [49-51] noted the importance of carefully selecting covariates and checking the balance of covariates with interaction effects, but because the treatment effect is not yet clear, this is seldom done in practice. Because IPTW directly uses propensity scores to control the bias caused by selection in outcome analysis, IPTW may be sensitive to model misspecification (i.e., when the covariates are inaccurate or omitted), and the distribution of weights and the covariate balance must be assessed. Some researchers have suggested that the distribution of weights (especially the average weight) should be evaluated to assess whether the conditioning model is correct and whether the model violates the relevant assumptions [45,52]. GBM is a strong nonparametric learning algorithm [53]. Many of its features are beneficial to propensity score methods. The regression tree, a basic classification algorithm, is iterated continuously to find the optimal function combination form and to prevent over fitting [54]. A smaller shrinkage coefficient can be used to reduce the variability. By optimizing the number of iterations and piecewise constant model, the variability of propensity score is reduced, and the generated weights are more uniform [44]. Therefore, it may be better to use IPTW with GBM to control confounding factors in the case of an unknown relationship between the treatment variable and covariates.
In the empirical study, GBM was superior to logistic regression in terms of ASAM and average weights in IPTW. Two variables remained imbalanced between the two groups by IPTW with logistic regression, whereas all variables were balanced by IPTW with GBM. The outcome analysis showed that the drug costs of outpatients with CHD with UEBMI were 256.35 Yuan higher on average than those of outpatients with URRBMI. The proportion of medical insurance reimbursement for urban employees is higher than that for urban-rural residents, which leads to higher demand for medical services. The basic purpose of medical insurance is to lighten the economic burden of disease on individuals and reflect fairness [55,56]. Therefore, the gap between different types of medical insurance must be narrowed [57,58]. Medical staff should standardize the behaviour of diagnosis and treatment and rationally used rugs to reduce the burden of patients, especially for patients with chronic diseases who take medicines for a long time. While ensuring the quality of medical care, it is responsible to help patients clarify relevant medical insurance policies and make rational use of health resources. This study focuses on the performance of logistic regression and GBM in propensity score weighting without considering other propensity score methods, and only the interaction effect and quadratic terms are included in this simulation study without higher-order polynomials. These considerations must be addressed in future research.
This work was supported by the Humanities and Social Science Project of Chongqing Municipal Education Commission, project number: 17SKG025.
- Guo S, Fraser MW (2015) Propensity Score Analysis Statistical Methods and Applications. 2nd Edition, Sage, California, USA. [Ref.]
- Jupiter DC (2017) Propensity Score Matching: Retrospective Randomization? J Foot Ankle Surg 56: 417-420. [Ref.]
- Bodily R, Larsen R, Warne RT (2018) Piecewise propensity score analysis: A new method for conducting propensity score matching with polytomous ordinal independent variables. Arch Sci Psychol 6: 14. [Ref.]
- Benedetto U, Head SJ, Angelini GD, Blackstone EH (2018) Statistical primer: propensity score matching and its alternatives. Eur J Cardiothorac Surg 53: 1112-1117. [Ref.]
- Peng Zhao, Xiaogang Su, Tingting Ge, Juanjuan Fan (2016) Propensity Score and Proximity Matching Using Random Forest. Contemp Clin Trials 47: 85-92. [Ref.]
- Ripollone JE, Huybrechts KF, Rothman KJ, Ferguson RE, Franklin JM (2018) Implications of the Propensity Score Matching Paradox in Pharmacoepidemiology. Am J Epidemiol 187: 1951-1961. [Ref.]
- Shida D, Ochiai H, Tsukamoto S, Kanemitsu Y (2018) Long-term outcomes of laparoscopic versus open D3 dissection for stage II/III colon cancer: Results of propensity score analyses. Eur J Surg Oncol 44: 1025-1030. [Ref.]
- Linden A, Yarnold PR (2018) Estimating causal effects for survival (time-to-event) outcomes by combining classification tree analysis and propensity score weighting. J Eval Clin Pract 24: 380-387. [Ref.]
- Andersen LW, Kurth T (2018) Propensity scores-A brief introduction for resuscitation researchers. Resuscitation 125: 66-69. [Ref.]
- Ko JH, Lee NR, Joo EJ, Moon SY, Choi JK, et al. (2018) Appropriate non-carbapenems are not inferior to carbapenems as initial empirical therapy for bacteremia caused by extended-spectrum beta-lactamase-producing Enterobacteriaceae: a propensity score weighted multicenter cohort study. Eur J Clin Microbiol Infect Dis 37: 305-311. [Ref.]
- Vetterlein MW, Gild P, Kluth LA, Seisen T, Gierth M, et al. (2018) Perioperative allogeneic blood transfusion does not adversely affect oncological outcomes after radical cystectomy for urinary bladder cancer: a propensity score-weighted European multicentre study. BJU Int 121: 101-110. [Ref.]
- Moik F, Riedl JM, Winder T, Terbuch A, Rossmann CH, et al. (2019) Benefit of second-line systemic chemotherapy for advanced biliary tract cancer: A propensity score analysis. Sci Rep 9: 5548. [Ref.]
- Kuss O, Blettner M, Börgermann J (2016) Propensity Score: an Alternative Method of Analyzing Treatment Effects. Dtsch Arztebl Int 113: 597-603. [Ref.]
- Austin PC, Stuart EA (2017) Estimating the effect of treatment on binary outcomes using full matching on the propensity score. Stat Methods Med Res 26: 2505-2525. [Ref.]
- Ahl R, Sarani B, Sjolin G, Mohseni S (2019) The Association of Intracranial Pressure Monitoring and Mortality: A Propensity Score- Matched Cohort of Isolated Severe Blunt Traumatic Brain Injury. J Emerg Trauma Shock 12: 18-22. [Ref.]
- Schneeweiss S, Eddings W, Glynn RJ, Patorno E, Rassen J, et al. (2017) Variable Selection for Confounding Adjustment in Highdimensional Covariate Spaces When Analyzing Healthcare Databases. Epidemiology 28: 237-248. [Ref.]
- Jackson JW, Schmid I, Stuart EA (2017) Propensity Scores in Pharmacoepidemiology: Beyond the Horizon. Curr Epidemiol Rep 4: 271-280. [Ref.]
- Ertefaie A, Asgharian M, Stephens DA (2017) Variable Selection in Causal Inference using a Simultaneous Penalization Method. J Causal Inference 6. [Ref.]
- David Lenis, Benjamin Ackerman, Elizabeth A Stuart (2018) Measuring Model Misspecification: Application to Propensity Score Methods with Complex Survey Data. Comput Stat Data Anal 128: 48-57. [Ref.]
- Waernbaum I, Pazzagli L (2017) Model misspecification and bias for inverse probability weighting and doubly robust estimators. Statistics Theory. [Ref.]
- Linden A, Yarnold PR (2017) Using classification tree analysis to generate propensity score weights. J Eval Clin Pract 23: 703-712. [Ref.]
- Harrell FE (2017) Regression Modeling Strategies: With Applications to Linear Models, Logistic regression and Survival Analysis. Springer 330. [Ref.]
- Gerasimovic M, Bugaric U (2018) Enrollment Management Model: Artificial Neural Networks versus Logistic Regression. App Artifi Intell 32: 153-164. [Ref.]
- Miller PJ, Lubke GH, McArtor DB, Bergeman CS (2016) Finding structure in data using multivariate tree boosting. Psychol methods 21: 583-602. [Ref.]
- Ridgeway G (2007) Generalized Boosted Models: A guide to the gbm package. [Ref.]
- Ding JM, Zhang XZ, Hu XJ, Chen HL, Yu M (2017) Analysis of hospitalization expenditures and influencing factors for inpatients with coronary heart disease in a tier-3 hospital in Xi’an, China: A retrospective study. Medicine (Baltimore) 96: e9341. [Ref.]
- Li C, Young BR, Jian W (2018) Association of socioeconomic status with financial burden of disease among elderly patients with cardiovascular disease: evidence from the China Health and Retirement Longitudinal Survey. BMJ open 8: e018703. [Ref.]
- Rosenbaum PR, Rubin DB (1983) The central role of the propensity score in observational studies for causal effects. Biometrika 70: 41- 55. [Ref.]
- Lunceford JK, Davidian M (2004) Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Stat Med 23: 2937-2960. [Ref.]
- Imbens GW (2004) Nonparametric estimation of average treatment effects under exogeneity: A review. Rev Econ Stat 86: 4-29. [Ref.]
- McCarthy RV, McCarthy MM, Ceccucci W, Halawi L (2019) Predictive Models Using Regression. In: Applying Predictive Analytics. Springer 89-121. [Ref.]
- Tu C (2019) Comparison of various machine learning algorithms for estimating generalized propensity score. J Stat Comput Simul 89: 708-719. [Ref.]
- Biau G, Cadre B, Rouvìère L (2018) Accelerated gradient boosting. Statistics, Machine Learning, Cornell University 1-18. [Ref.]
- Batra M, Agrawal R (2017) Comparative Analysis of Decision Tree Algorithms. In: Panigrahi BK, Hoda MN, Sharma V, Goel S (eds) Nature Inspired Computing: Proceedings of CSI 2015. Springer 31- 36. [Ref.]
- Basha SM, Rajput DS, Vandhan V (2017) Impact of Gradient Ascent and Boosting Algorithm in Classification. Int J Intell Eng Sys 11: 41- 49. [Ref.]
- Li X, Lu J, Hu S, Cheng KK, De Maeseneer J, et al. (2017) The primary health-care system in China. Lancet 390: 2584-2594. [Ref.]
- McCaffrey DF, Ridgeway G, Morral AR (2004) Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychol Methods 9: 403-425. [Ref.]
- Stürmer T, Rothman KJ, Avorn J, Glynn RJ (2010) Treatment effects in the presence of unmeasured confounding: dealing with observations in the tails of the propensity score distribution--a simulation study. Am J Epidemiol 172: 843-854. [Ref.]
- Jacqueline M Burgette, John S Preisser, R Gary Rozier (2016) Propensity Score Weighting: An Application to an Early Head Start Dental Study. J Public Health Dent 76: 17-29. [Ref.]
- Xin M (2018) Comparison of propensity score technique and applied in pharmacoeconomic. Chongqing medical university.
- Fullerton B, Pöhlmann B, Krohn R, Adams JL, Gerlach FM, et al. (2016) The Comparison of Matching Methods Using Different Measures of Balance: Benefits and Risks Exemplified within a Study to Evaluate the Effects of German Disease Management Programs on Long-Term Outcomes of Patients with Type 2 Diabetes. Health Serv Res 51: 1960-1980. [Ref.]
- Abdia Y, Kulasekera KB, Datta S, Boakye M, Kong M (2017) Propensity scores based methods for estimating average treatment effect and average treatment effect among treated: A comparative study. Biom J 59: 967-985. [Ref.]
- Pirracchio R, Petersen ML, van der Laan M (2015) Improving propensity score estimators’ robustness to model misspecification using super learner. Am J Epidemiol 181: 108-119. [Ref.]
- Lee BK, Lessler J, Stuart EA (2010) Improving propensity score weighting using machine learning. Stat Med 29: 337-346. [Ref.]
- Austin PC, Stuart EA (2015) Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat Med 34: 3661-3679. [Ref.]
- Austin PC, Stuart EA (2017) The performance of inverse probability of treatment weighting and full matching on the propensity score in the presence of model misspecification when estimating the effect of treatment on survival outcomes. Stat Methods Med Res 26: 1654-1670. [Ref.]
- Linden A (2017) Improving causal inference with a doubly robust estimator that combines propensity score stratification and weighting. J Eval Clin Pract 23: 697-702. [Ref.]
- Parast L, McCaffrey DF, Burgette LF, de la Guardia FH, Golinelli D, et al. (2017) Optimizing Variance-Bias Trade-off in the TWANG Package for Estimation of Propensity Scores. Health Serv Outcomes Res Methodol 17: 175-197. [Ref.]
- Alam S, Moodie EEM, Stephens DA (2019) Should a propensity score model be super? The utility of ensemble procedures for causal adjustment. Stat Med 38: 1690-1702. [Ref.]
- Franklin JM, Shrank WH, Lii J, Krumme AK, Matlin OS, et al. (2016) Observing versus Predicting: Initial Patterns of Filling Predict Long- Term Adherence More Accurately Than High-Dimensional Modeling Techniques. Health Serv Res 51: 220-239. [Ref.]
- Lunt M (2014) Propensity analysis in Stata revision: 1.1. [Ref.]
- Setodji CM, McCaffrey DF, Burgette LF, Almirall D, Griffin BA (2017) The Right Tool for the Job: Choosing Between Covariate-balancing and Generalized Boosted Model Propensity Scores. Epidemiology 28: 802-811. [Ref.]
- de Menezes SF, Liska GR, Cirillo MA, Vivanco MJF (2017) Data classification with binary response through the Boosting algorithm and logistic regression. Expert Sys Appl 69: 62-73. [Ref.]
- Griffin GA, McCaffrey D, Almirall D, Setodji C, Burgette L (2017) Chasing balance and other recommendations for improving nonparametric propensity score models. J Causal Inference 5: 20150026. [Ref.]
- Liu X, Liu Z, Wang G, Cai Z, Zhang H (2017) Ensemble transfer learning algorithm. IEEE Access 6: 2389-2396. [Ref.]
- Zhang Y, Dong D, Xu L, Miao Z, Mao W, et al. (2018) Equity in health care after 10 years of the New Rural Co-operative Medical Insurance Scheme in China: an analysis of national survey data. Lancet 392: S35. [Ref.]
- Yang C, Huang Z, Sun K, Hu Y, Bao X (2018) Comparing the Economic Burden of Type 2 Diabetes Mellitus Patients with and without Medical Insurance: A Cross-Sectional Study in China. Med Sci Monit 24: 3098-3102. [Ref.]
- Yong M, Xianjun X, Jinghu L, Yunyun F (2018) Effect of health insurance on direct hospitalisation costs for in-patients with ischaemic stroke in China. Aust Health Rev 42: 39-44. [Ref.]
Download Provisional PDF Here
Article Type: RESEARCH ARTICLE
Citation: Wang Y, Xie J, Liu X, Du J, Wu M, et al. (2019) Logistic Regression and Generalized Boosted Modelling in Inverse Probability of Treatment Weighting: A Simulation and Case Study of Outpatients with Coronary Heart Disease. J Epidemiol Public Health Rev 4(3): dx.doi. org/10.16966/2471-8211.178
Copyright: © 2019 Wang Y, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
SCI FORSCHEN JOURNALS
All Sci Forschen Journals are Open Access
