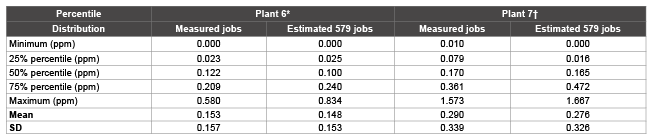
Table 1: Distribution of measured and estimated styrene concentrations in two study plants (1976-1985)
* Plant 6 had 22 measured jobs with 144 measurements
† Plant 7 had 44 measured jobs with 704 measurements

Xuguang (Grant) Tao*
Division of Occupational and Environmental Medicine, Department of Medicine, Johns Hopkins School of Medicine, Baltimore, USA*Corresponding author: Xuguang (Grant) Tao, Division of Occupational and Environmental Medicine, Department of Medicine, Johns Hopkins School of Medicine, Baltimore, USA, E-mail: xtao1@jhmi.edu
The estimation of chemical exposures for unmeasured jobs is a well-recognized problem in occupational epidemiologic studies. This paper has described a simple Z-score method and its application in providing styrene concentration estimations by job and plant for a case cohort study on styrene exposure and ischemic heart disease as an example. This method of estimation assumes that the relative exposure of a job was similar across the industry because tasks associated with the job are similar, but individual plants may have overall differences in the actual levels of the chemicals. The exposure for an unmeasured job in a specific plant could be estimated based on the relative exposure level of that job from other plants and the concentration distribution parameters of measured jobs form the same plant. This method has overcome some disadvantages of existing methods for concentration estimation for unmeasured jobs.
Exposure assessment; Missing values; Occupational; Styrene; Z-score
In occupational epidemiological studies, measurement data are not always available for all jobs. Estimation of pollutant exposures when jobs are unmeasured is a well-recognized problem in occupational data [1]. The following methods have been used to resolve the problem by investigators: 1) One commonly used method to deal with the problem is to ask industrial hygienists to give each unmeasured job an exposure estimation category or so-called industrial hygienist’s rank (IH rank) based on their knowledge and experience. Exposure categories (high, medium and low) or IH ranks (ranging from 0 to 10) can be used as relative exposure indicators in risk analysis [1-4]. The assumption behind this method is that the relative exposure of a job is similar across the industry because tasks associated with the job are similar. The advantage of this method is that it can provide a relative exposure indicator by job in the analysis. One problem with this method is that it ignores potentially large variations in exposure concentrations for the same job among plants, if different plants are included in the study population. A job ranked at 5 can actually have a higher exposure to a chemical in one plant than the same job in other plants. In other words, a job ranked at 5 in a “dirty” plant could have an actual concentration level which is similar to a job ranked at 8 in a “clean” plant. Risk analysis based on this exposure assessment system would possibly have misclassification problem. 2) If measurement data are used, a common method is to use an average concentration of the pollutant at the same job from other plants as concentration estimation for the unmeasured job. This method also ignores the variations in exposures of the same job among different plants. Utilizing the exposure from other plants for an unmeasured job in a specific plant may also alter the relative orders of all jobs in terms of exposure levels within that plant, since the measurements from other plant could be systematically higher or lower than that in the particular plant. 3) Another method is proportional interpolation [5]. Exposure concentration at an unmeasured job in Plant A is estimated using the exposure concentration of the same job in Plant B multiplying the ratio of the mean concentrations of available measurements in Plant A versus Plant B. The advantage of this method is that it takes the variation of the mean exposure concentrations among different plants into account. The problem is that the distribution parameters of concentrations such as a standard deviation in Plant A are assumed the same as Plant B, which is not true in most circumstances. 4) Another method is deterministic modeling [6-8]. If the significant factors determining the level of exposure can be identified and assessed, a deterministic model can be used to calculate the exposure. The advantage of this method is that it can be used without measurement data. The problem is that the identification and the data collection of these significant determinants are difficult and the result is likely to be less reliable than a measurement based estimation.
This paper describes a simple method, Z-score method, which has been used to provide styrene and butadiene concentration for unmeasured jobs in part per million (ppm) by job and plant for a case cohort study on styrene exposure and ischemic heart disease [9]. This method is designed to overcome some mentioned disadvantages of above existing methods for concentration estimation for unmeasured jobs.
Let us start with a simple example. Assuming there is a distribution with a mean of 0.5 and a standard deviation (SD) of 0.2, one can easily tell that a point value at 1.5 times SD above the mean is 0.8. What does this example tell us? Firstly this example shows that any point value in a distribution can be presented by a difference or distance from the mean and this difference can be presented by a proportion of the SD of the distribution. This difference of a point value from the mean presented by a proportion of the SD is so called “Z-score” or “standard score” [10,11]. In other words, a Z-score is a measure of the distance from the mean of a distribution normalized by the standard deviation of the distribution. In above example, 1.5 is the Z-score of the point value of 0.8 in a distribution with a mean of 0.5 and a SD of 0.2. Mathematically a Z-score of a point value can be obtained by using Formula A. Secondly this example also shows that given the mean and SD of a distribution as well as a Z-score of a point value, one can easily tell what the original point value would be, using formula B, which is a reverse format of the formula A. In above example, for instance, the original point value, 0.8, can be easily calculated given a Z-score of 1.5, a mean of 0.5, and a SD of 0.2. Therefore, one can fill an unknown point value in a distribution as long as the mean and SD of the distribution is known and the relative position of the point can be identified.
$$Z\, = \,{{X\, - \bar X} \over {SD}}..............\left( A \right)$$
$$X\, = \,Z\,.\,SD\, + \,\bar X..............\left( B \right)$$
Where
Z: Z-score of a point concentration;
X: A point concentration value;
X : Mean of the distribution;
SD: Standard deviation of the distribution.
Mathematics of Z-score transformation and its reverse are simple and straightforward. However, what makes this method unique and even more interesting is the feature of Z-score distribution. If all point values of a distribution are transferred into Z-scores, the distribution of Z-scores has necessarily a constant mean of zero and a standard deviation of one [10,11]. In other words, Z-score transformation converts distributions with different means and SDs into a standard distribution with a constant mean of zero and a standard deviation of one. What is more, although the Z-scores, means, and SDs are more meaningful in a normal distribution than in other distributions, the normality of the original distribution is not necessary for using Z-score transformation to create a standardized distribution with a constant mean of zero and a standard deviation of one. What the Z-score transformation does is just subtracting a constant from the each point value and dividing the result by another constant, so that the relative order of point values is consistent but scaled differently. What make this feature import is that since Z-score distributions always have a constant mean of zero and a standard deviation of one and the relative order of point values is consistent, Z-scores from different distributions will be comparable to each other although the original point values from distributions with different magnitudes, ranges, or units are not comparable. In other words, a Z-score is a standardized indicator of relative positions of original point values so that point values with similar relative positions in their own distribution will have similar Z-scores. Therefore, the Z-scores of point values are interchangeable across different distributions, if their relative positions are similar.
According to above description, how this Z-score method can be used in estimating a concentration for an unmeasured job becomes clear. In order to estimate a chemical concentration for an unmeasured job in a plant, based on Formula B, one has to known: 1) the distribution parameters, the mean and SD of that chemical distribution, in that plant. The mean and SD in the plant can be estimated based on the concentrations of measured jobs in that plant assuming those measured jobs are a representative sample of all jobs in that plant and 2) a relative exposure indicator in the distribution, the Z-score of that unmeasured job. Since the concentration for that job in that plant is not measured, one can’t get a Z-score of that job in the same plant. However, based on the feature of Z-score, Z-scores for the same job in other plants should be similar, assuming that the relative exposure of that job is similar across the industry because tasks associated with the job is similar although absolute exposure may vary by plant. In this case a Z-score of the same job from other plants can be used as the Z-score of the job in the particular plant. In case that the concentration for the job is not measured in any of the plants, the Z-score is not based on measurements but the IH rank for that job as an alternative, since IH ranks are designed to represent relative exposures. A Z-score transformation of IH ranks is necessary to make the distribution comparable with measurement based Z-score distributions. However, the usefulness of IH rank based Z-scores is dependent on number of categories which are designed in the IH rank system. A 0-10 ranking system would be better than a high-median-low ranking system in using this method.
There is one thing which needs to be pointed out. When the Z-scores for a job are available from more than one information source, a weighted average Z-score may be calculated. The weights for different information sources, including measurements and IH ranks, should be determined by investigators based on the validity and reliability of each source. However, if the assumption, that the relative exposure of a job is similar across the industry because tasks associated with the job is similar, is true, the Z-scores for that job from different sources should be similar to each other although absolute exposure may vary by sources.
A case-cohort study on styrene exposure and ischemic heart disease (IHD) included 498 cases who died from IHD and a sub-cohort of twice that size, 997, selected as a 15 percent random sample of the total male cohort who were ever employed in two styrene-butadiene polymer manufacturing plants between 1943-1982 [9]. In order to establish a doseresponse relationship between styrene exposure and IHD, the tasks of exposure assessments for the case-cohort study included 1) styrene and butadiene concentration estimation for unmeasured job and 2) exposure adjustment for change over time. The Z-score method introduced in this paper was used for the first task of the two and only the styrene estimation for unmeasured jobs for the first task will be introduced as an example here.
Although not all unmeasured jobs were needed to be estimated in this case-cohort study, we did not know in advance which set of jobs would be involved, thus we estimated the styrene concentration for all unmeasured and measured jobs among the total 579 jobs in the job dictionary developed for this industry in previous studies [2-4]. Each of these 579 jobs was assigned a unique job code, which was a combination of the codes for the subdivision, the work area, the sub area, and the job title for that particular job. All jobs were reviewed by a group of expert industrial hygienists and engineers from the industry as well as academia to determine the accuracy of the job classifications. These experts then were asked to rank each of the jobs on the job code list from 0 to 10 for both styrene and butadiene. The estimates were made based on the personal experience of these engineers, most of who had worked in the industry from its inception. The actual number of unique jobs involved in the job histories of the subjects in this study was only 166 out of the 579.
Measurement data were collected for many of the jobs from different sources such as NIOSH, the International Institute of Synthetic Rubber Producers, and the participating plants in previous studies. Out of the eight plants studied previously [2-4], only five plants provided styrene measurements. Four of the five plants with styrene measurement were US plants, including the two plants involved in the case-cohort study, Plant 6 and 7. In order to use all of the available measurement information, all measurements from four US plants were used to get information on the relative exposure, Z-scores, for each job. The available measurement data for each plant were used to provide the mean and SD of measurements for transferring Z-scores back to concentrations for unmeasured jobs based on the method introduced above.
In the calculation of an average Z-score, the weight for a measurement Z-score is the number of measurements for that job from that information source over the sum of all weights. The weight for an IH rank Z-score is 1 over the sum of all weights. The sum of all weights for an average Z-score was the total number of measurements + 1. This weighting system relied more on the measurement data than on IH rank.
The exposed concentration for an unmeasured job in a plant was estimated based on the relative exposure value of the job, an average exposure Z-score for the job, and the actual mean and SD of measured values in the plant. Actually the estimations were done for measured job too. However, in the analysis the observed value would override the estimated value if the observed concentrations were available. The estimated concentrations were only used for unmeasured jobs.
The estimation took the following steps
After these steps were done, each of all 579 jobs in each plant had an estimated concentration. It is difficult to show the estimation for each of the 579 jobs by plant in this paper. As a summary, however, Table 1 shows the percentile distributions of measured and estimated data for the two plants, Plants 6 and 7, which were involved in the case-cohort study. The means and SDs for measured job, 0.153 and 0.157 for Plant 6 and 0.290 and 0.339 for Plant 7, as well as average Z-score from other Plant and IH ranking were used to determine the unique estimated concentration for each job by plant. The distribution of the estimated concentrations for 579 jobs is similar to the distribution of available measured jobs by comparing their percentiles, means, and SDs. The ranges of the concentration are a little bit wider in estimated data than measured data. The numbers of measured jobs were small in the two plants. Table 2 summarizes the numbers of measurement used for calculation of average Z-scores, mean average Z-scores, and estimated mean styrene concentrations by IH rank and Plant. In addition to Plants 6 and 7, the results for Plants 1 and 4 have also been listed to show that although average Z-scores are the same for the same jobs, each plant has kept their own original distribution with different means and SDs of concentration for all estimated concentrations.
The concept and conduct of this methodology are very simple. It can be very useful, however, in occupational epidemiological studies as an exposure assessment alternative for unmeasured jobs. The method has overcome the disadvantages of existing methods as discussed in the introduction section. It puts both relative exposure for a job and the concentration distribution of all jobs in the particular plant into account. However, this method still has limitations. One of the two major assumptions of the method is that the relative exposures among these jobs are similar across the industry because tasks associated with those jobs are similar although the absolute exposure levels can be very different. Generally, this assumption is the same as that of IH ranking system and may be true. That is why the IH rank method has been so popular in occupational epidemiologic studies. However, it is possible that there are some jobs with changes that are not proportional to others in different plants. Misclassification could be an issue if the assumption did not stand. The other important assumption of this method is that the limited measurements on limited number of jobs in a plant are representative of the concentrations of all jobs in that plant so that the distribution parameters obtained from these limited number of jobs can be applied for all jobs in that plant. This assumption may not be true, 1) if the jobs are not randomly picked or those jobs with higher exposures might be measured more. However, if all plants had the same tendency to select more exposed jobs, would the influence of the issue might not that big, when applying Z-score from other plants for an unmeasured job in a particular plant? This should be investigated further and 2) if the numbers of the measured jobs are too small to obtain stable means and SDs even if the jobs are randomly picked for measurement. In the example of this paper both issues might exist. Anyway, one has to have some measurements in a plant to obtain the distribution parameters so that Z-score can be used to estimate concentrations for unmeasured jobs for that plant. Without any measurements, one cannot use this method. The other issue may rise when only IH rank is available for Z-score calculation. Since IH ranks are categorical, Z-scores of IH ranks are not continuous. For instance, a 0-10 ranking system will only have 11 Z-score values at the best. Sometimes, not all ranking categories are used by the experts as in the example study. For instance, rank 5, 7, and 9 were not assigned to any job (Table 2), so that a possible 11 level ranking system had actually only eight categories in this case. The estimation based on this categorical system would be less precise than that based on measurements.

Table 1: Distribution of measured and estimated styrene concentrations in two study plants (1976-1985)
* Plant 6 had 22 measured jobs with 144 measurements
† Plant 7 had 44 measured jobs with 704 measurements
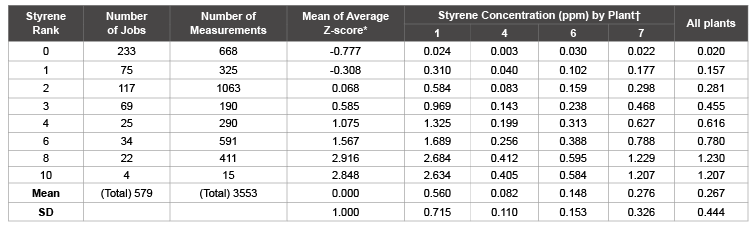
Table 2: Estimated average concentration (ppm) by rank for four US plants
* Mean of average Z-scores of jobs within the rank
† Mean of estimated styrene concentrations of jobs within the rank
It should be pointed out that the method introduced here is used for cross-sectional concentration estimations. The concentration change over time was not considered. However, this method can be also used for concentration estimation by time period given enough information on the dimension of time. For instance, if you have measurement data by different time period, means and SDs for the different periods would be used in the concentration estimation for different period of time [9].
Download Provisional PDF Here
Article Type: Review Article
Citation: Tao X (2016) A Method to Estimate Concentrations of Chemicals for Unmeasured Jobs. J Epidemiol Public Health Rev 1(2): doi http://dx.doi. org/10.16966/2471-8211.113
Copyright: © 2016 Tao X. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
All Sci Forschen Journals are Open Access