
Full Text
Echu Liu*
Department of Health Management and Policy, Saint Louis University, Saint Louis, MO 63104, USA*Corresponding author: Echu Liu, Department of Health Management and Policy, Saint Louis University, Saint Louis, MO 63104, USA, Tel: (314) 977-1304; E-mail: echuliu@slu.edu
Observational studies often suffer from the self-selection problem which is due to the non-randomness of selecting objects into treatment and control group. As result, the precise estimation of treatment effect becomes impossible by relying on a conventional approach, such as ordinary least squares (OLS) regression. Many researchers in public health use propensity-score matching to correct the bias related to selfselection problem in order to obtain the exact estimate of treatment effect. However, propensity-score matching is not a panacea for self-selection problem. This article explains why sometimes propensity-score matching may not work, and gives empirical researchers in public health a gentle introduction to other methods, which is not so well-known in the field, for correcting self-selection problem.
More and more empirical researchers in public health are interested in evaluating the effects of treatment, such as policy, services, or procedures, using observational data. There are several advantages of using observational data to study treatment effect, such as less time and energy spent on collecting the data by the researcher and a larger sample size for study. However, one of the disadvantages of observational study, which is always a concern to many empirical researchers, is the potentially biased estimate of effect. The source of this bias is the non-randomness of selection of the objects into the “treatment group, with which refers to the objects in the dataset that are impacted by some policies, receive certain services, or undergo certain procedures. The non-random selection eventually leads to the non-comparable treatment group and control group, which is named “self-selection problem” in the literature, and a simple comparison of the average outcome of interest of these two groups, will lead to a misleading estimate of the treatment effect. This is because there is no way to know if the difference in the average outcomes—if there is a difference, and if it is significant in a statistical sense—is due to the treatment or the inherent differences between these two groups.
In order to obtain an unbiased estimated treatment effect in observational studies, Rosenbum PR and Rubin DB [1] proposed an approach, which is called “propensity-score matching,” to take the fundamental differences existing between treatment and control groups into consideration when doing estimation. The idea is as follows. If the inherent differences between treatment group and control group can be defined based on a vector of “observable” characteristics, then we would be able to calculate a score for each object in the study based on this vector and only include those observations with identical scores when taking the differences between the average outcome of interest, because these observations will be “comparable” based on this score. As a result, the bias will be eliminated after controlling the scores, which are named “propensity-score” in the literature.
The approach proposed by Rosenbum PR and Rubin DB [1] is straightforward, and several pieces of statistical software, including STATA, have user-written modules that can implement this approach. However, there are a couple of concerns and considerations when it comes to implementation. First, the number of observable characteristics that should be included when computing the propensity-score is always a challenging decision. Second, it is almost impossible for any researcher to find the observations in the treatment and control groups with identical propensity-scores, especially when the number of variables included for computation of propensity score increases. All interested readers can refer to Becker SO and Ichino A [2] for a more detailed discussion of these issues and potential solutions.
Based on my interaction with many empirical researchers in public health so far, many of them assume that using propensity-score is a panacea to the self-selection problem. However, as mentioned in the previous section, it was assumed by Rosenbum PR and Rubin DB [1] that the differences between treatment group and control group are due to some observable characteristics. This means that if the differences between treatment and control groups are also due to some unobserved characteristics, such as preferences, then the approach proposed by Rosenbum PR and Rubin DB [1] will be inappropriate1 .
When the differences between treatment and control groups are due to observable and unobservable characteristics of the observations, the estimation of the treatment effect is still possible. For instance, if the dataset used by researchers is only one year, the most intuitive way to estimate the effect of a treatment indicator ti (equals to 1 if the observation belongs to the treatment group; otherwise equals to 0) is to run the following regression by controlling a vector of observable characteristics xi using this data '
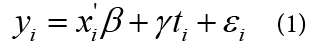
where yi is the dependent variable, εi is the error term, β is a vector of coefficients, γ is a coefficient defining treatment effect, and the subscript i refers to the ith observation. If there exist some unobservable factors that influence an individual’s decision to receive the treatment, and these variables are obviously not able to be controlled in equation (1), then they will be hidden in εi . Consequently, the correlation between ti and εi will be unequal to zero, and the estimate of γ in ordinary least square (OLS) will no longer be the precise estimate of “real” effect of ti on yi , because the OLS estimate of γ will combine the direct effect of ti on yi and indirect effect of unobservable factors on yi . Also, the statistical tests of significance of the coefficient estimate of β and γ could suffer from Type I or Type II error.
A potential solution to the problem of self-selection due to unobservables is instrumental variables (IV) regression. This approach has been widely used in many applied areas of economics to estimate treatment effect, but is less well known by scholars in public health. The idea of IV regression can be explained by using equation (1) as an example. Assume there exists a vector of variables, . zi zi determines ti , but only affects yi through its effect on ti . In other words, zi is correlated with ti but uncorrelated with εi . Then the IV regression can be carried out in two steps. In the first step, a regression of ti on i x and zi is performed, and the predicted value ti ϒ ˆ ti is computed. In the second step, ti in equation (1) is replaced by ˆ ti and a regression of yi on xi and ˆ ti is performed, and the resulting coefficient estimate of ϒ will be an unbiased estimate of treatment effect. The intuition behind IV regression is explained as follows. Since the correlation between ti and εi in equation (1) is not equal to zero when the problem of self-selection due to unobservables exists, replacing ti with ˆ ti which is computed based on variables that are uncorrelated with εi in equation (1) will eliminate the correlation between ti and εi and makes precise estimation of coefficient ϒ possible. Cameron and Trivendi [3] provides a gentle introduction to the IV regression and the intuition behind it, and most statistical software packages have commands that can be used to conduct the IV regression.
Although IV regressions are intuitive and easy to implement, it can sometimes be difficult to find valid IV. When obtaining IV is infeasible, another possible solution to the problem of selection due to unobservables is estimating a fixed-effects model with panel data (if available). Panel data refers to a dataset in which we observe characteristics of subjects at several different points in time, i.e., we have several observations on the same subjects, and the simplest fixed-effect model with panel data can be depicted as in equation (2)
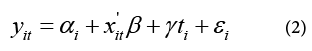
where subscript i refer to ith observation and subscript t refers to tth period. αi Is an individual-specific parameter that is time-invariant and serves as a proxy for the unobservable heterogeneity among individuals. Therefore, a panel fixed-effect model allows us to control for unobserved characteristics of the subjects in order to obtain a precise estimate of the effect of ti .
In general, there are two approaches we can follow to estimate a panel fixed-effect regression model such as equation (2), including firstdifferencing and least-square dummy variables (LSDV). Cameron and Trivendi [3] gives an easy-to-understand explanation of the assumptions and implementation of these two approaches. Most software packages for statistics, including SAS and STATA, have commands that can be used to perform these two approaches. However, it needs to be kept in mind that it does not matter which approach is followed, any short panel (few time periods and many individuals) dataset is not suitable for the panel fixed-effect model, because this model exploits the time dimension of the subjects to control for the unobserved. If the time dimension is not high enough, then αi in equation (2), for example, is not identified.
It is impossible to establish a laboratory like in natural sciences and run experiments in observational studies. As a consequence, the results from much of the work done related to estimation of treatment effect are biased since it suffers from non-randomness of selection into treatment and control group. The purpose of this article serves as a reminder to the empirical researchers in public health that, depending on the assumption about the source of non-randomness (“selection on observables” versus “selection on unobservables”), the statistical methods that can be applied are different. Propensity score matching is just one of these methods. Additionally, discussion of some more advanced statistical methods for treatment evaluation, such as difference-in-differences (DID) and regression discontinuity design, are not covered in this paper. Interested readers can refer to Cameron and Trivedi [4].
- Rosenbum PR, Rubin DB (1983) The central role of the propensity score in observational studies for causal effects. Biometrika 70: 41-55. [Ref.]
- Becker SO, Ichino A (2002) Estimation of average treatment effects based on propensity scores. The Stata Journal 2: 358-377. [Ref.]
- Cameron AC, Trivedi PK (2010) Microeconometrics using Stata. Stata Press, College Station TX. [Ref.]
- Cameron AC, Trivedi PK (2005) Microeconometrics: methods and applications. Cambridge University Press, New York NY. [Ref.]
Download Provisional PDF Here
Article Type: Short Communication
Citation: Liu E (2016) Propensity-Score Matching as Panacea for Correcting Self-Selection Bias in Observational Studies. J Epidemiol Public Health Rev 1(2): doi http://dx.doi.org/10.16966/2471-8211.109
Copyright: © 2016 Liu E. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
SCI FORSCHEN JOURNALS
All Sci Forschen Journals are Open Access
