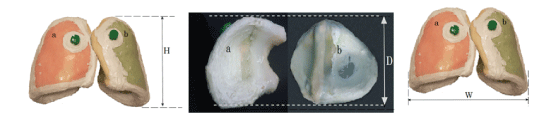
Figure 1: The dimensions of the anatomical lung phantoms a). The right lung b). The left lung (Height: H=23 cm, Width: W=28 cm and Depth: D=13.7 cm).


Khoramdel R Hsseinimotlagh SN* Parang Z
Department of Physics, Shiraz Branch, Islamic Azad University, Shiraz, Iran*Corresponding author: Hsseinimotlagh SN, Department of Physics, Shiraz Branch, Islamic Azad University, Shiraz, Iran, E-mail: hosseinimotlagh@ hotmail.com
The use of Radiation Therapy (RT) in lung cancer has shown some exciting and sometimes disappointing advances in recent years. Protons compared with photons interact differently with human tissues, and can be used to improve patient care suffering lung cancer. A new strategy is the simultaneous injection of Nanoparticles (NPs) with proton radiation to the tumor which has been given over a decade to improve conventional RT. In this work, Proton Beam Therapy (PBT) with Gold Nanoparticles (GNPs) is used as part of a combination program for the treatment of advanced localized lung cancers. The purpose of this paper is developing the complex GEANT4 (G4) model on the human lung and predict the distribution of absorbed dose in lung tumors during proton therapy without and with high-Z injection of GNPs. Thus, the distribution of the absorbed dose in lung tumor for four modes of Bethe-Bloch’s relativistic quantum theory, G4 simulation model, hartree-fock-roothaan wave functions and the bortfeld theoretical model without and with the injection of GNPs in predicted phantom of the lung are compared.
Proton; Relativistic; Simulation; NPs; Lung
Lung cancer is one of the leading cancers around the world. Lung cancer is categorized into two main categories, depending on the appearance of cancer cells: Non-Small Cell Lung Cancer (NSCLC) and Small Cell Lung Cancer (SCLC). Most importantly, due to the difficulty of treating lung cancer, to a large extent, this cancer can be considered as the most common type of cancer that can lead to death, both in men and in women. It is important to know which type of lung cancer is affected, because small cell cancers have the best response to chemotherapy, while other types, often referred to as large lung cancers, and are better treated with surgery or radiotherapy [1]. RT using photon radiotherapy (XRT) has been a standard treatment for lung cancer since the 1960s [2]. Despite years of research, the result is that treating patients with lung cancer is generally weak due to their cancer tendency to metastasis using XRT. Therefore, studying on a more precise treatment of lung cancer is essential. A potential way to improve the outcome of the disease is optimization RT. Historically, the patient’s therapeutic outcome is improved if newer radiation patterns are invented. For the first time, radiotherapy was performed through radioisotopes that were directly inserted into the tumor. This was a problem when treating lung cancer from the moment of placing the source in a lung tumor and caused physical damage to the lung. Subsequently, low-energy x-rays were produced that brought KV X-rays into the lung cancer tissue. Unfortunately, these rays penetrated slightly into tissuesand deposited the maximum dose to the skin, and deposited only a small fraction of the dose to the tumor. Then, the cobalt isotope with atomic number of 60 was used and gamma rays with two distinct energies of 1.17 and 1.33 Million Volts (MV) were produced and passed through the skin and resulting in deeper penetration of the dose. Then linear accelerators were developed that produced X-rays or photons with MV energy. These photonic beams penetrated better, but still had deposited a maximum dose between1.5 to 3.5 cm, which gradually decreased the amount of absorption during penetration, so that the radiation without stopping directly was transmitted out of the body. The distribution of X-rays in the body is due to their unique characteristics, which are almost massless and without charge. First, accelerated protons with a large amount of momentum enter to the body, which they can carry a specific depth depending on their initial kinetic energy that is given them by the accelerator (cyclotron or synchrotron). As the PB moves to this depth, a relatively small amount of energy is transmitted to the tissue, and gradually, the protons slow down more and more energy is transmitted to the surrounding tissues. The lost energy per unit path length is proportional to the inverse of the square velocity of proton. Shortly before the total proton energy is wasted, the rate of energy loss reaches a sharp peak. When the kinetic energy of the proton is completely deposited in the tissue, the proton inside the body can be rest. The energy of protons in collision with the electrons of neighboring atoms in the surrounding tissues leads to their ionization and thus causes radiation damage. A region in the body where the maximum energy is wasted and the final stop of the protons occurs is narrow at a certain depth depending on the initial energy of the proton beam. This sharpness and peak, which represents the maximum dose due to the charged particles, is called “Bragg Peak”. Beyond this point, as the protons stop, no radiation energy effects on the surrounding tissues. So far, we have just talked about mono energetic proton beams. But the peak of the mono energetic PB is very narrow therefore to produce a useful clinical PB for the complete coverage of the tumor it is required that in the high-dose area is spread which known as the “spread-out Bragg peak”. Clinical data are necessary to prove the success of the patient’s delivered dose to improve the patient. In the newer proton therapy, uses pencil beam scanning instead of passive scattering and uniform scanning pencil beams are very narrow proton beams that are driven by magnetic fields and move forward and backward in a chess pattern inside the tumor volume. Recently, the use of NPs (NPs) has been suggested as a more effective criterion to improve tumor targeting through radiation effects. When the tumor containing the NPs is exposed under the beam of the proton beam, the antibodies or peptides forming the tumor cells are affected. Therefore, a combination of radiotherapy with nanomedicine opens up a new range of therapies. Hainfeld JF, et al. in 2008 showed that a core of GNPs with a diameter of 1.9nm increases the life time of mice exposed to X-rays of 160 kV [3]. GNPs are already well-known. Other advanced NPs that were made from other heavy elements, such as hafnium [4] and gadolinium [5], which were made by Nanobiotix (Paris, France) and NH TherAguix (Villeurbanne, France), were recently sent to clinics. The effectiveness of high-Z NPs was shown by Kim JK, et al. to improve the proton radiation performance [6]. They injected small NPs (diameters of 1.9-14nm) from gold or iron into tumors of mice that were simultaneously exposed by fast protons with energies of 45MeV and observed that the absorbed dose in the tumor and, consequently, the killing of cancer cells are increased. The efficiency of GNPs has been confirmed by Polf JC, et al. in increasing the effects of proton radiation through the laboratory [7]. The group observed a significant increase in the mortality of prostate tumor cells with 160MeV protons when loaded with GNPs. Recent molecular scale experiments with platinum and gadolinium NPs that have been activated by 150MeV protons [8]. Butterworth KT, et al. in 2008 [9], Porcel E, et al. in 2010 [10], Jain S, et al. in 2014 [11] examined the simulation of three matter suitable treatments such as gold (Au), silver (Ag) and platinum (Pt) such that all of them are compatible with each other and can be used for treatment [11]. Since nanomaterials with high Z can increase the deposited dose in the tumor due to the increase of secondary electrons, we also use simultaneous injection of NPs of three substances (gold, silver and platinum) and proton radiation in the treatment of lung cancer. We will optimize the conditions relative to the state where NPs are not used. For this purpose, in section 2 introduces the characteristics of the suggested phantom used in this study. In sections 3,4 and 5, absorbed dose, amplification of radiotherapy by injecting GNPs into the tumor and the Bethe-Bloch model in a completely relativistic state are introduced., respectively. In the sections 6,7 and 8, Nuclear and electronic stopping power, hartree-fock-roothaan atomic wave functions and Bragg-Kleemaan’s law governing on the PT are given, respectively. In sections 9,10,11, multiple coulomb scattering, proton range and range straggling are defined, respectively. In section 12, bortfeld model is described, and finally the conclusions are identified.
Phantom of the lung tissue is designed to accurately represent the shape and size of the human lung. The dimensions of the lung phantom are: height 23 cm, width 28 cm and depth 13.7 (Figures 1 and 2). The G4 toolkit, version 9.2.02, was chosen as the simulation engine. The water phantom with homogeneous geometry and dimensions 30 × 30 × 40 cm3 was used to simulate G4. Dimension x (the beam penetration axis) is determined as the maximum range for proton therapy. The matrix with size of 1 × 1 × 1 mm3 is set to achieve the results of the data. The entire space, with the exception of phantom, is filled with air. At a depth of 10 cm inside the phantom, a cubic tumor is placed in a size of 2 cm. Adipose and skin tissue is defined in thicknesses of 0.3 cm and 0.2 cm, respectively.

Figure 1: The dimensions of the anatomical lung phantoms a). The right lung b). The left lung (Height: H=23 cm, Width: W=28 cm and Depth: D=13.7 cm).
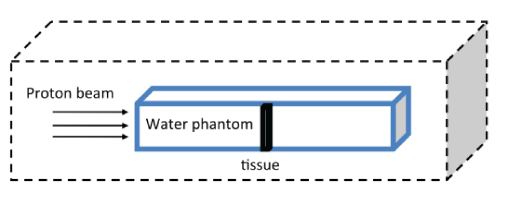
Figure 2: A plan for the selected phantom used in this study.
The phantom material in this geometry is taken from the National Institute of Standards and Technology (NIST). This data provides a detailed mix of materials based on the International Commission on Radiation Units (ICRU). Physical models include electromagnetic and nuclear processes. Electromagnetics physics mainly provides the ionization and multiple scattering of each particle based on Lewis’s theory for the proton. This theory calculates the spatial distribution as the angular distribution after a stage [12]. Low-energy processes, up to 250 electron volts for photons and electrons, like hadrons and ions, are implemented through multiple models. From electromagnetic physics model based on ICRU49 is used for simulation [13].
Nuclear interaction physics is used to study the elastic and inelastic collision between protons and materials. Elastic scattering contributes to the low energy transmission of proton beams while the inelastic scattering contributes to the interaction of nucleon-nucleon along the path of the proton beam. The G4 Pre compound model is used for simulation in nuclear physics. This model is suitable for explaining the interaction in the PB energy range and is a good estimation for the production of secondary and neutrons particles because it allows the expansion of the low energy range of the hadron kinetic model to inelastic collision of the nucleus-nucleon. For this simulation, the PB is used in the energy range 3 ≤ E(MeV) ≤ 250MeV, with Gaussian distribution σ(E) in the water phantom. The produced gaussian distribution is compared with the distribution of the simulated and measured dose in the water phantom, respectively. The proton source is a pencil beam scanning type that is located at 10 cm far from the upper level of the water phantom. The proton source is parallel to the axis of the beam, (the x axis), and 5 × 10 6 particles are simulated in our calculations. All particles are examined as if their range exceeds the specified threshold of 0.01mm, to be identified. The location of the bragg peak is the maximum dose point of the curve. The range is defined as the distance between the entrance surface of the beam and the 80% of distal point of the dose in g/cm2.
In this paper, we focus on the amount of absorbed dose, which is defined as the deposited energy per unit mass of the matter and is given by:
Where Edep is a deposited energy, ρ is the mass density and V is the volume of absorbing matter. The absorbed dose D is a physical quantity and does not reflect the biological effects of radiation. However, D is the first step in assessing the environmental impact of radiation, both for accidental and definitive effects. The Monte Carlo simulation (MC) is known as a required method for the study of nuclear medicine physics, radiology and RT. The deposited energy and absorbed dose have attracted special interest to radiotherapy programs [14] and imaging programs involving ionizing radiation [15]. In radiotherapy (RT), treatment planning requires an accurate assessment of the distribution of the absorbed dose in the target organ and tissue. Many MC simulators for imaging [16-18] or dosimetry, [19-24] have been developed. At present [25], GATE7 (G7) [26] is the only MC simulation platform that supports imaging, RT and dosimetry in the same environment. G7 is an application G4 toolkit that simulates particles and matter, and G7 provides high-level features to facilitate the design of G4-based simulations. The G7 is developed by OpenG7 and is a community-based initiative that each user can access the source code [27] and offer some new features. The G7 is essentially useful for a wide range of simulations, including those working on absorbed dose. Despite the fact that G7 has been widely accepted and used for a variety of PET and SPECT studies, there are still a limited number of articles that have been used this kind of code in dosimetry. The G7 is provided with a mechanism called Actor Dose that stores the absorbed dose in a specific volume in a 3D matrix. From the point of view of macro-scale G7, Actor Dose should be linked to the volume of case study. The user can determine the size of the matrix and the matrix location is defined in the system of coordinated volumetric control.
Note that if the user defines the matrix size larger than the associated volume, deposited absorbed dose occurs outside this volume and therefore will not be recorded inside the network. The Actor calculates the deposited energy (Edep) in MeV and the absorbed dose, D, in Gy. The squares of Edep and D are summed and can be used to compute statistical uncertainty when the simulation is split into several branches. Equation (2) defines the statistical uncertainty εk in pixel k, for N value, which represents the initial number of events. dk is the deposited energy in pixel k in the initial event i. The absorbed dose can be calculated as the dose in water, which is commonly used in radiotherapy, and the dose in the medium is commonly used in MC simulations [28,29]. This conversion is done by taking into account the relative stopping power and energy transferred through nuclear interactions in a given environment. Note that this conversion method may not be appropriate for some conditions in brachytherapy [30].
During particle tracking, the deposited energy is added in the matrix for each stage occurring in the connected volume. The two endpoints a step, are a pre and a post points. For a charged particle, a location is randomly selected along the step and values are stored in the matrix at that location. The user must be sure that the length of the step is not very large due to the matrix sampling. The output can be stored in an MHD image format, consisting of a header and a raw data file. The effect of calibration of Hounsfield Units (HU) on materials and density has also been reported in reference [31]. At G7, the user can manually assign a substance to any HU range, or use schneider’s method based on a predefined material group (24 materials by default). Two mixtures with the same elemental composition, but different densities are considered as two distinct materials. Each requires the calculation of the cross-section and the stopping power, and if a lot of materials are used, it can be problematic. In reference [32], the authors described a method for dynamically changing the density at run-time, but this technique is still not available in G7. In G7, the number of materials can be controlled by the tolerance parameter [33]. It is used to decompose a substance into two substances when its HU range is greater than tolerance (Table 1).
| Tissues | ρ(g/cm3) | H | C | N | O | Na | P | S | Cl | K | Au |
| Skin | 1.090 | 10.00 | 20.40 | 4.20 | 64.50 | 0.20 | 0.10 | 0.20 | 0.30 | 0.10 | - |
| Soft Tissue | 1.03 | 10.5 | 25.6 | 2.7 | 60.2 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 | - |
| Lung | 0.29 | 10.30 | 10.50 | 3.10 | 74.90 | 0.20 | 0.20 | 0.30 | 0.30 | 0.20 | - |
| Tumor | 1.040 | 9.40 | 21.20 | 5.60 | 61.50 | 0.25 | 0.51 | 0.64 | 0.39 | 0.51 | - |
| 10mgAu/ml | 1.05 | 10.6 | 14.4 | 2.2 | 70.5 | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 1.0 |
| 25mgAu/ml | 1.07 | 10.4 | 14.2 | 2.1 | 69.5 | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 2.3 |
| 50mgAu/ml | 1.09 | 10.2 | 13.8 | 2.1 | 67.9 | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 4.6 |
| 75mgAu/ml | 1.12 | 10.0 | 13.5 | 2.1 | 66.4 | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 6.7 |
Table 1: The elemental composition and mass densities of some human tissues.
In targeted cancer treatment, physicians use drugs that can better penetrate cancer cells to diagnose and treat. For this purpose, GNPs are used as a photon active element simultaneously with PB irradiation. RT by mixing NPs increases the number of photoelectrons in the tumor due to the presence of particles with a high atomic number. As the absorption of photoelectrons into the irradiated tumor increases, the absorbed dose of the tumor enhances. Experimental studies have shown that the size of NPs and how they are distributed in different organs are related with each other. The maximum accumulation of GNPs with diameters of 20-100 and 220nm is in the liver and spleen, but NPs smaller than 10nm in diameter were observed in most organs including kidney, heart, lung, brain, liver and spleen. NPs used in medicine are classified into two main groups. The first group of particles that contain organic molecules as the main building material and the second group that usually contain metals and minerals as the core, NPs (eg GNPs) are commonly used simultaneously with particle therapy to kill cancer cells due to their compatibility with the biological system and their low toxicity. One of the most important parameters of NPs is the choice of their synthesis method. Because the physical and chemical properties of the particles depend on it and is selected according to the type of coating agent, appropriate stabilizer and the desired size. In order to use GNPs biologically, their surface must be functionalized, which is called functionalization. The functionalization of NPs is done with the aim of smartening, insensitivity of the immune system and reducing toxicity in the body.
Depending on the application of functionalized NPs, different agents and compounds are used. For example, GNPs can be functionalized with polyethylene glycol to reduce toxicity, escape from the immune system and as a result, have a longer durability in the bloodstream [8]. Another important feature of GNPs is their easy coupling with antibodies. Therefore, GNPs are injected into the patient’s body in various ways, such as intravenous injection or injection at the tumor site. In a healthy tissue, endothelial cells have a regular arrangement and an impenetrable distance for NPs, but in a tumor tissue, the arrangement of endothelial cells is irregular and has large pores, which causes high GNPs permeability to tumor tissue. In this process, the antibodies first guide the NPs to the target cells and after attaching them to the target cells, they are irradiated. All cancer cells that interact with the NPs and are killed by the heat generated with the collision of electromagnetic waves caused by the radiation of a particle beam with GNPs.
We do not discuss the bethe-bloch model in detail, but just examine the aspects of this model for proton therapy. The average energy loss rate per unit length of a relatively relativistic heavy charged particle is described in detail by the bethe-bloch equation: [34]
The symbols used in this equation are shown in table 2, respectively. In a low-energy region (less than 10MeV), when the particle velocity is equal to one of the target electrons (≈0.0073c), ion neutralization due to electron capture plays a crucial role in the stop process, and z must be converted to Zeff, which a semi-experimental relation Zeffz(1-exp(125zβ-2/3)) has been extracted from darks experimental data. In figures 3a-h, using the maple programing, we plotted the three-dimensional variations of different parameters such as β = v/c, barkas correction, shell correction, lindhard-sorensen correction [35] density effect, the effective atomic number, the total stopping power and absorbed dose in terms of the energy of the PB in the range of 1 ≤ E(MeV) ≤ 250 and the depth of penetration in the lung tissue in the range of 1 ≤ x(cm) ≤ 30 without the injection of NPs of metal. As shown in the diagrams, each parameter plays a specific role in the calculation of the stopping power and absorbed dose, and they are a function of the depth of the proton penetration in the tissue and the energy of the proton.
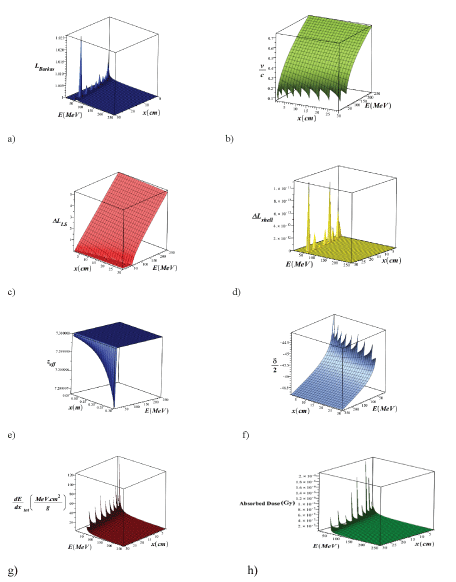
Figure 3: 3D variations of β =v/c, Barkas correction, shell correction, Lindhard-Sorensen correction, density effect, effective atomic number, total stopping power and absorbed dose, in terms of PB energy in the range of 1E (MeV) ≤ 250 and the penetration depth in the lung tissue in the range of 1 ≤ x (cm) ≤ 30 without the injection of metal NPs (using Equation 3).
Table 2: List of parameters in the Bethe-Bloch equation.
An energetic ion that penetrates the material loses its energy mainly through two processes that are independent of each other. These two processes are: loss of nuclear energy and loss of electron energy. Thus, the stopping power can be divided into two parts: i) nuclear and ii) electronic stopping power. Nuclear stopping power is calculated by integrating over all of the impact parameters:
Where
According to figure 4, the ion with mass of M1 and initial energy E0 is deflected by the target atom with mass of M2. The location of M2 relative to M1 is called the impact parameter, which we represent it by b. During the collision, M1 and M2 deflect with the angles α and β, respectively, relative to the original M2 pathway. During the collision, the kinetic energy, T, it transfers from M1 to M2. According to momentum and energy conversation, this transmitted kinetic energy can be calculated. This kinetic energy T is a function of the angle α, projectile energy, E0, projectile mass M1 and the mass of target atom M2 in the laboratory system.
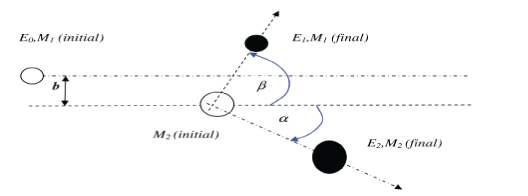
Figure 4: A plan indicating an ion with mass M1 and initial energy E0 that collides to an atom with mass of M2 and causes it to move with energy E2 and to reduce its E1 energy.
The electronic stopping power in this region is given by the bethebloch equation:
In figure 5, we plotted the variations of total mass stopping power
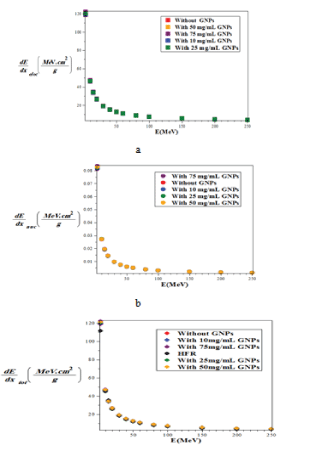
Figure 5: Comparison of the mass-stopping power a) electronic b) nuclear c) total of proton with and without injection of GNPs with different concentrations in the lung phantom and comparison with the Hartree-Fock-Roothaan (HFR) [37] atomic wave function model without Injection of GNPs using the G77/G4 simulation.
The hartree-fook method is based on the time independent model of the particle. The idea behind this model is to solve the Schrödinger equation for moving electrons in nuclear potentials and the potential of all the other electrons. This repetition continues until the density of the resulting electron charge converges with the electron charge density at start point for one repetition. The hartree-fock-roothaan atomic wave functions are the solutions of hartree-fook’s equation and are represented by the orbital of Slater -type:
In this equation di is the expansion factor of the orbital. Λi(r ) , is the orbital of slater -type and is characterized by the following equation:
Here, Ni is the constant of normalization and ni is the principal quantum number and αi is the exponent value of the orbital.
From the observation and comparison of the graphs shown in figure 5, the minimum of stopping power in all three cases of nuclear, electronic and total, is related to without NPs of gold. By increasing the concentration of GNPs, the amount of all type of the stopping power gradually and slightly increases.
Also, for all modes of without and with the injection of GNPs, with increasing proton energy, all of the stopping powers are reduced and the minimum stopping power is related to the nuclear interactions. The electronic stopping power is much higher and the main contribution of the total stopping power can be electronic term. Also the total stopping power of without the injection of GNPs using the model of hartree-fock-roothaan (HFR) atomic wave functions are consistent with the G4 simulation model. In figure 6, the absorbed dose in the lung phantom was compared to with and without the injection of GNPs in terms of the depth of penetration in the tissue for various proton energy (GNPs is a sphere with a diameter of 50nm). As shown in figures 5 and 6, with increasing proton energy, stopping power and absorbed dose decrease, but by increasing the concentration of GNPs their amount goes up. This is due to the production of secondary electrons. It is seen that from figures 6a-d, with increasing distance and energy, from the beginning of the lung phantom, the absorbed dose at the Bragg peaks is reduced, and the location of the bragg peak moves with increasing energy to higher x-rays. And the lowest amount of absorbed dose is the related to without injection of GNPs. By increasing the amount of GNPs injection from 10 to 75mg/ml, the amount of absorbed dose increased by 1.1, 1.25, 1.45 and 1.75% for 10,25,50 and 75mg/ml, respectively in comparison to without injection ofGNPs. This is due to the fact that high-Z NPs, such as NPs of gold, increase the amount of doses deposited inside a tumor or matter due to the increase of secondary electrons and the effect of density. And with an assumption that the tumor is at a depth of 13 cm inside the lung with a width of 2 cm, the optimum energy of the bragg peak is 93MeV. Our calculations also show that when protons have energy of 250MeV, they require a phantom with a radius of more than 30 cm, so that the protons deposited their energy inside it, and only protons with energy in the range of 80 to 95MeV deposited their energy inside the selected phantom.
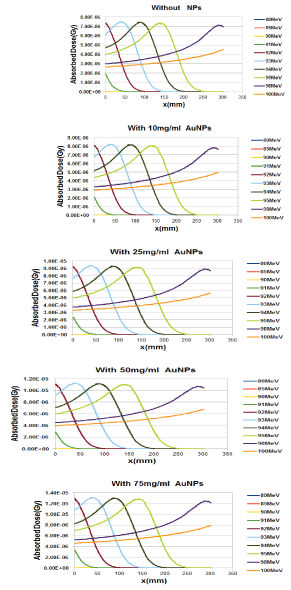
Figure 6: Comparison of the absorbed dose in the lung phantom with or without the injection of GNPs in terms of penetration depth for various proton energy (GNPs are considered as a sphere with a diameter of 50 nm and for this calculation we use G7/G4 simulation).
The Bragg-Kleemaan law for the proton range, R0, is given in terms of the initial energy E and energy curve dE/dx with the following relation:
Where α and p, can be determined from the bethe equation or from a model that is fitted with the win-energy data, which their values are: α=0.00262, p=1.736. In figure 7, we plotted the three-dimensional variations of proton mass stopping power and absorbed dose in a lung tissue without the injection of GNPs using the bragg-kleemaan law in terms of PB energy in the range of 1 ≤ E(MeV) ≤ 250 and the penetration depth in the range 1 ≤ x(cm) ≤ 30.
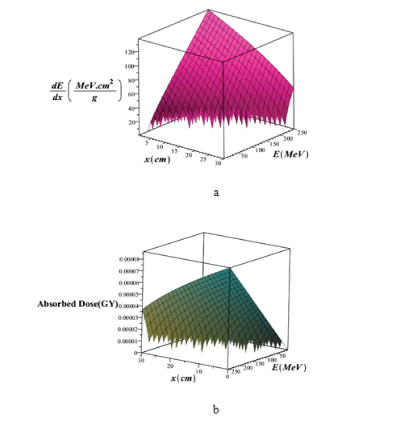
Figure 7: Three-dimensional variations of a) total mass stopping power and b) absorbed dose in lung tissue without injection of GNPs using Bragg-Kleemaan law in terms of proton energy in the range of 1 ≤ E (MeV) ≤ 250 and the penetration depth in the lung tissue in the range of 1 ≤ x (cm) ≤ 30.
From the comparison of the graphs for the stopping power of the Bethe-Bloch (Figure 3g, using Maple programing) with the model of the hartree-fock-roothaan (HFR) wave functions [36] and the model of proposed phantom of the lung in this work (Figure 5C using G4 simulation) without the injection of GNPs we found that these models confirm each other.
Transitory protons of matter may be deflected by the atomic nucleus, a process commonly referred to scattering, more precisely, multiple coulomb scattering, when observed that angular scattering due to the collective effect of many small single scattering randomly happens. Both protons and nucleus are positively charged particles, as a result, are the interaction between them mainly electrostatics. The multiple Coulomb scattering theory describes the shape of the angular distribution of the particles and its characteristic width. Moliere’s theory gives directly root mean square of multiple coulomb scattering angles at each incident energy for homogeneous slabs of each element with very thin thickness to near stopping thickness. The mean scatter angle θ0 is determined by the highland relation:
Where p and v are the momentum and velocity of the proton, respectively, z is the atomic number of projectile, and L and LR are the target thickness and radiation lengths, respectively which are the same unit. This formula is valid for a thin slab. The radiation length is the distance which the energy of the radiation particles decreases due to radiation losses as much as the coefficient e-1 (≈ 0.37). In figure 8, we plotted the variations of the mean coulomb scattering angle in terms of proton energy in the range of 1 ≤ E(MeV) ≤ 250 for with and without the injection of different concentrations of GNPs in the lung phantom.
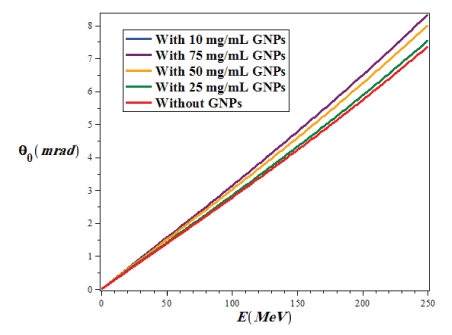
Figure 8: The variations of the mean Coulomb scattering angle in terms of proton energy in the range of 1 ≤ E (MeV) ≤ 250 for with and without the injection of different concentrations of GNPs in the lung phantom.
As we can see from figure 8, with increasing the proton energy, the mean value of the coulomb scattering angle (θ0) increases in all conditions, but the lowest θ0 in the lung tumor is related to the state of the without injection of GNPs, while with increasing the amount of injection of GNPs into the lung tumor the value of θ0 gradually increases.
In this work, we use the CSDA method to calculate the proton range. CSDA is calculated by integrating on the initial and final energy of the incident particle on the inverse of the total stopping power, which is given by the following: [37]
Here, E0 and Ef are the initial and final energy of the charged particle input at the target. In figure 9, we plotted the proton range variations in terms of proton energy in the range of 3 ≤ E(MeV) ≤ 250 without and with the injection of GNPs in the lung tissue and these diagrams were compared with the results of Hartree-Fock-Roothaan (HFR) [36,37] wave functions model.
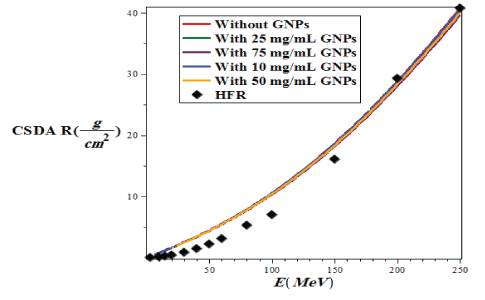
Figure 9: Variations of CSDA proton in lung tissue with and without injection of GNPs using G4/G7 simulation based on the energy of the PBs in the range of 1 ≤ E (MeV) ≤ 250 and the penetration depth in the range of 1 ≤ x (cm) ≤ 30 and compare it with the model of HartreeFock-Roothaan (HFR) wave functions [37].
As shown in figure 9, the lowest CSDA range is related to the case of without injection GNPs, and with increasing the amount of the concentration of injection gold nanoparticle, the CSDA has slightly increased such that at 75mg/ml of GNPs in the lung tissue the CSDA is maximized and in good agreement with results of the hartree-fockroothaan (HFR) wave functions model.
The loss of energy of an ion in matter is a statistical process and it is not definite, and the Bethe equation yields only the energy lost. This change was first described by bohr, who introduced the concept of energy straggling (σE):
Where ρe is the electron density and ϵ0 is the vacuum permittivity coefficient. This is valid for energy dissipation that is large enough to maintain Gaussian approximation. But it is small enough when ion energy can be assumed to be constant. In 2004 schulte and his colleagues gave the following differential equation: [38]
Where K(x) is as follows:
The range straggling (σR) is defined as a function of energy is given by the solution of the following equation:
Where S(E) is the total mass stopping power. We calculate the range straggling in terms of proton energy in the lung tissue for two case of without and with the injection of GNPs, and plot it in figure 10.
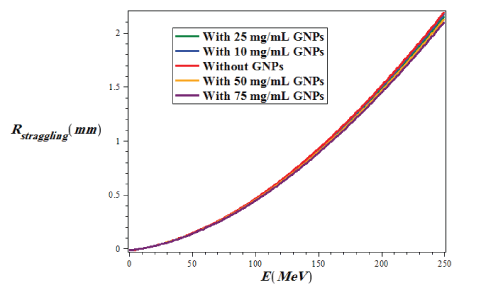
Figure 10: Variations of proton range straggling in lung tissue for two states of with and without injection of GNPs using G4/G7 simulation versus the energy of a PB in the range of 1 ≤ E (MeV) ≤ 250 and the penetration depth in the range of 1 ≤ x (cm) ≤ 30.
As shown in figure 10, the range straggling increases with increasing proton energy for both modes of with and without the injection of GNPs, but the highest range straggling is for the case of without injection of GNPs and the lowest amount is related to injection of GNPs at a concentration of 75mg/ml. In fact, if the amount of injection of GNPs is more and more, the straggling range decreases.
The bortfeld model is based on the Continuous Slowing Down Approximation (CSDA) with additional features that are not considered in the bethe bloch model. In different cases, it is appropriate to have an analytical representation of the bragg curve instead of using numerically or measured data. The 1997 brownfield paper provides an approximate analysis of the bragg curve in a closed form. The validity of this model is based on proton energy between about 10 and 200MeV. The four main principles of this model are: a power-law relation that describes the energy-range dependence, a linear model for reducing flounce due to columbic nuclear interactions, assuming a fraction of localized released energy, a gaussian approximation of the distribution of the range straggling and the presentation of the energy spectrum of multi-energy beams with a Gaussian distribution with a linear “tail” [39] (Figure 11).
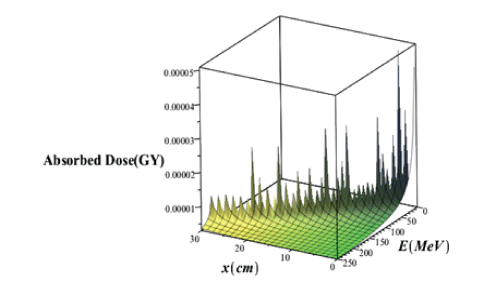
Figure 11: Three-dimensional variations of the deep dose without considering the effects of the proton straggling range in terms of the penetration depth and energy of the proton beam.
From this theoretical model two types of deep doses are achievable:
a. Deep dose formula without examining the effects of proton straggling range is: [39]
Note that the above equation is valid for z<R0, For z>R0, D(z)=0.The above equation can be written as a sum of two terms:
The first term Da(z) is the contribution of dose due to proton without nuclear interactions. The second term, Db(z) represents the dose transmitted by a relatively small fraction of protons having nuclear interactions.
b. Deep dose with the straggling range of the proton’s effects is: [39]
Some of the “special functions” and the parameters that appear in equations (18) to (20) are defined as follows:
Geiger’s law is: R0=αEp0 the range R0 is determined by the exponent dependence on energy E0, where p and α are constant. In ICRU 49, p=1.77, but the bragg-kleeman law describes the constant α. According to geiger’s law, the proton traverses the maximum range of R0 in initial energy E0 . Therefore, in the energy E(x) along x (direction of motion), the proton travels the distance R0 -x, which is the same as the solutions of the weber’s differential equation. Γ(z) is the gamma function defined by euler’s formula. The functional relationship between σ and R0 can be given with the following approximation:
Where α′ is a factor which depends on the stopping matter through α. R0 and σ are in cm. In the borteff model, γ is the fraction of energy that is locally absorbed. In this model, γ=0.6 and β≈0.012 cm-1. 𝜑0 is the particle flouncethat is the number of particles per cm2. Suppose ζ=R0-x/σ. In figure 12, the three-dimensional variations of absorbed dose with the effects of the proton straggling in terms of the penetration depth and energy of the PB in the lung tissue without the injection of GNPs has been brought.
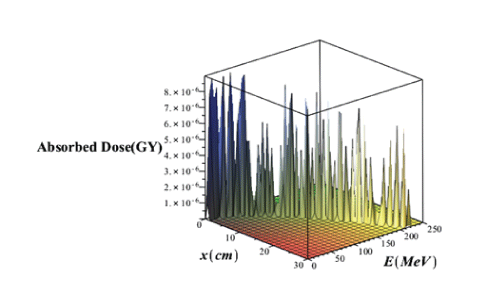
Figure 12: Three Dimensional variations of absorbed dose with considering effects of proton straggling range versus the penetration depth and energy of the PB without injection of GNPs.
Comparison of figures 11 and 12 it is seen that in the case of without injection of GNPs, the absorbed dose value taking into account the effects of the range straggling, is less than the amount of absorbed dose regardless of the absorption effects. Comparing the absorbed dose diagram using completely theoretical quantum relativistic BetheBloch model with the Maple programming in figure 3 and the absorbed dose diagram without the injection of GNPs through the proposed phantom G4/G7 simulation in figure 6 and the absorbed dose diagram using bragg-kleemaan law with maple programming in figure 7b and absorbed dose diagram using bertfeld model without considering effects of proton range straggling using maple programming in figure 11 and absorbed dose diagram using bertfeld considering the effects of proton range straggling using maple programming in figure 12, we find that bragg’s peak only seen in the bethe-bloch model and G4/G7 simulation model of the proposed phantom, and the values ofabsorbed dose from each purposed modelare different, but this difference is not so much, and the proposed G4/G7 simulation model is more complete than the other models, also the results of this proposed model confirm that injection of GNPs into the lung tumor increases the absorbed dose and the enhancement ofconcentration of the GNPs increases the value ofabsorbed dose.
In this review, we summarize the current status of the PBT(PBT) for lung cancer. The proton source is a hydrogen nucleus and the proton is accelerated by an accelerator. The proton is stopped at a certain depth, known as the Bragg peak, which significantly reduces the outlet dose and reduces damage to healthy tissues around tumor volume. These proton therapeutic properties can be useful in the treatment of lung cancer in patients with cardiovascular disease, with poor pulmonary function or history of previous breast cancer therapy. This work has examined a number of research topics related to proton therapy issues that are important for optimizing the future of cancer treatment. Proton therapy is an important tool in the oncology period, where the RT goal is to treat a tumor with a minimum toxicity and maximum efficiency. Proton therapy is not expected to be uniform in all scenarios for all patients, but it is expected to dosage be done in such a way that the patient achieves superior clinical results at appropriate times. The proton beams are sensitive to various types of uncertainty, such as respiratory motion, changes in the patient’s location and tumor contraction. But the new proton therapy technology creates a major challenge in radiotherapy planning and delivering. And further research is needed to optimize protons, especially for new beam systems. This requires more understanding of physics to create designs that are strong in the face of uncertainties. Therefore, in the following we described briefly the future challenges and outlook for this work. From the very basic knowledge of photoelectric and related effects it can be easily concluded, that there are clearly benefits in combining GNPs with radiotherapy. Here likewise much work is still necessary in order to optimize not only the multi-parameter properties mentioned above, but also to predict the most efficient way in secondaries production. It was already shown that the surface modifications, which increase the cellular uptake and make the passive or active targeting possible, may cap the secondary electrons in the close vicinity of the NP, thus preventing an efficient radio sensitisation. This implies that some new compromises between what has been known to work and the aimed actions must be explored. There is a great amount of both experimental and theoretical work devoted to all possible parameters of NPs. Such great variability of sizes, shapes, and coatings associated with the differential cellular responses dependent on cancer types makes it at the moment difficult to establish any correlations or standard conditions for treatments; therefore, some clarification and organization of the achievements of various communities must be done.
Combining the excellent sparing of healthy tissue of proton therapy with the enhanced biological effect within the tumor from the use of GNP, offers the potential for improved patient outcomes. It is important to note that the simultaneous combination of high-energy proton beams and the injection of GNPs into cancerous tissue in the human lung have not yet occurred, whereas it has contracted in the cancerous tissue of mice and had promising results. Clinical results in the human lung have not been reported yet and require more experience, and our work only provides simulation results.
Download Provisional PDF Here
Article Type: RESEARCH ARTICLE
Citation: Khoramdel R, Hsseinimotlagh SN, Parang Z (2022) Comprehensive Study of Lung Cancer Proton Therapy with Injection of GNPs. J Clin Case Stu 7(1): dx.doi.org/10.16966/2471-4925.250
Copyright: © 2022 Khoramdel R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
All Sci Forschen Journals are Open Access